课  题

函数与方程

课  型

复习课

课  时

第 1  课时

主备课人

周思

复备课人

陈雄武

审核人

雷淇未

课前准备

教 学 目 标

（1）结合二次函数的图象，了解函数的零点与方程根的联系，判断一元二次方程根的存在性及根的个数。

（2）根据具体函数的图象，能够用二分法求相应方程的近似解。

教学重点

函数与方程的零点

教学难点

函数与方程的零点

教学过程和教学内容

二次备课

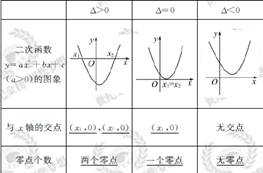
一、基础回扣

1.函数零点

(1)定义:对于函数y=f(x)(x∈D),把使_______的实数x叫做函数y=f(x)(x∈D)的零点.

(2)函数零点与方程根的关系:方程f(x)=0有实根⇔函数y=f(x)的图象与____有交点⇔函数y=f(x)有_____.

(3)零点存在性定理:如果函数y=f(x)在区间[a,b]上的图象是_________的一条曲线,并且有_____________,那么函数y=f(x)在区间(a,b)内有零点,即存在x₀∈(a,b),使得_______.

2.二次函数y=ax²+bx+c(a>0)的图象与零点的关系

3.二分法

(1)二分法的定义

(2)用二分法求函数零点近似值的步骤.

二、典例突破

考向 1 函数零点的求解与判断 

【典例1】(1)函数f(x)=2^x+x³-2在区间(0,1)内的零点个数是　(　　)

(A)0　　　(B)1　　　(C)2　　　(D)3

(2)(2013·湛江模拟)设函数y=x³与y=(1/2)^x-2的图象的交点为

(x₀,y₀),若x₀∈(n,n+1),n∈N,则x₀所在的区间是　　　　

考向 2 二分法及其应用 

【典例2】(1)在用二分法求方程x³-2x-1=0的一个近似解时,现在已经将根锁定在区间(1,2)内,则下一步可断定该根所在的区间为________.

(2)函数f(x)=x³+x²-2x-2的一个正数零点附近的函数值如下(精确度0.1):

那么方程x³+x²-2x-2=0的一个近似根(保留3位有效数字)为_____.

考向 3 函数零点的应用 

【典例3】已知函数f(x)=-x²+2ex+m-1,g(x)=x+(x>0).

(1)若g(x)=m有实数根,求m的取值范围.

(2)确定m的取值范围,使得g(x)-f(x)=0有两个相异实根.

【易错误区】忽视定义域导致求函数零点个数失误 

【典例】(2012·湖北 )函数f(x)=xcos x²在区间［0，4］上的零点个数为

(A)4     (B)5     (C)6        (D)7

三、知能巩固

1.(2012·北京高考)函数f(x)= -()^x的零点的个数为(　　)

(A)0　　(B)1　　(C)2　　(D)3

2.设方程log₄x-(  )^x=0，          =0的根分别为x₁，x₂，则(   )

(A)0＜x₁x₂＜1     (B)x₁x₂=1

(C)1＜x₁x₂＜2      (D)x₁x₂≥2

3.(2013·日照模拟)已知x₀是函数f(x)=+lnx的一个零点,若x₁∈(1,x₀),x₂∈(x₀,+∞),则(　　)

(A)f(x₁)<0,f(x₂)<0　   (B)f(x₁)>0,f(x₂)>0

(C)f(x₁)>0,f(x₂)<0     (D)f(x₁)<0,f(x₂)>0

四、课时作业

教学札记：