| 上传:admin | 审核发布:admin | 更新时间:2015-3-22 17:23:08 | 点击次数:772次 |
勾股定理导学案
学习目标: 1.会用勾股定理解决简单的实际问题。
2.树立数形结合的思想。
3,经历探究勾股定理在实际问题中的应用过程,感受勾股定理的应用方法
重点:勾股定理的应用
![]() 难点:实际问题向数学问题的转化
难点:实际问题向数学问题的转化

![]()
1, 直角三角形有那些特征?
(1)有一个角是_______的三角形。
(2) 两个锐角__________的三角形。
(3) 如果直角三角形的三边长a、b、c有关系式_________________
(4)在含30°角的直角三角形中,______________________
![]()
1,阅读探究1,探究2体会 勾股定理在实际问题中的应用
2,数轴上的点能表示有理数,你能在数轴上表示无理数吗?如何表示?利用什么定理?
![]()
1.小明和爸爸妈妈十一登香山,他们沿着45度的坡路走了500米,看到了一棵红叶树,这棵红叶树的离地面的高度是 米。
2.如图,山坡上两株树木之间的坡面距离是4![]() 米,则这两株树之间的垂直距离是
米,则这两株树之间的垂直距离是
![]() 米,水平距离是 米。
米,水平距离是 米。
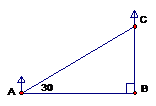
2题图 3题图
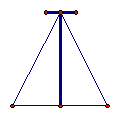
3.如图,一根12米高的电线杆两侧各用15米的铁丝固定,两个固定点之间的距离是 。

![]()
![]()
(一) 基础知识探究
 探究点一
探究点一
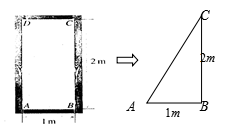
例1:在长方形ABCD中,宽AB为1m,长BC为2m ,求AC长.
问题(1)在长方形ABCD中AB、BC、AC大小关系?
(2)一个门框的尺寸如图1所示.
①若有一块长3米,宽0.8米的薄木板,问怎样从门框通过?
②若薄木板长3米,宽1.5米呢?
③若薄木板长3米,宽2.2米呢?为什么?
【分析】1,在(1)(2)的基础上将(3)的实际问![]() 题转化为数学模型:木板的宽2.2米
题转化为数学模型:木板的宽2.2米
大于1米,不能横着过,,木板的宽2.2米大于2米,不能竖着过;只能试斜着过
2,要斜着过,应求什么?
3,要求AC,根据什么定理?
例2:(4)如图2,一个3米长的梯子AB,斜着靠在竖直的墙AO上,这时AO的距离为2.5米.
① 球梯子的底端B距墙角O多少米?
② 如果梯的顶端A沿墙下滑0.5米至C,请同学们猜一猜,底端也将滑动0.5米吗?
③ 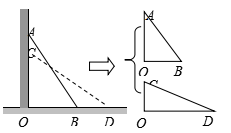 算一算,底端滑动
算一算,底端滑动![]() 的距离近似值(结果保留两位小数).
的距离近似值(结果保留两位小数).
分析】(1)在Rt△OAB中,由图得 AB=_____,AO=_____,
则根据勾股定理求BO=_______
(2)由AO-AC得到CO的长,在Rt△OCD中运用勾股定理
求出OD的长![]() ,再由OD-OB得出BD的长
,再由OD-OB得出BD的长
例3. 问题:我们知道数轴上的点有的表示有理数,有的表示无理数,你能在数轴上表示出
![]() 的点吗?
的点吗?![]() 的点呢?
的点呢?
分析:我们只能找到数轴上的表示有理数的点,而对于象![]() 和
和![]()
![]() 这样的无理数却找不到如果
这样的无理数却找不到如果![]() 能画出长为
能画出长为![]() 和
和![]() 的线段,就能在数轴上画出表示
的线段,就能在数轴上画出表示![]() 和
和![]() 的点。容易发现长为
的点。容易发现长为![]() 的线段可以看作是两条直角边为1的直角三角形的斜边,长为
的线段可以看作是两条直角边为1的直角三角形的斜边,长为![]() 的线段可以看作是两条直角边
的线段可以看作是两条直角边![]() 为2、3的直角三角形的斜边。
为2、3的直角三角形的斜边。
步骤:在数![]() 轴上找到点A,使OA=_____,作直线l垂直与OA在l上取点B,使AB=_____,以原点O为圆心,以OB为半径作弧,弧与数轴的交点C即为表示
轴上找到点A,使OA=_____,作直线l垂直与OA在l上取点B,使AB=_____,以原点O为圆心,以OB为半径作弧,弧与数轴的交点C即为表示![]() 的点。
的点。
应用迁移,巩固提高
问题:(1)根据勾股定理,还可以作出长为无理数的线段,你能作出哪些长为无理数的线段呢?
(2)欣赏下图,你会得到什么启示?
(3)你还能找到其他作长为无理数的线段的方法吗?
教师重点关注:能否将无理数转化为某个直角三角形的斜边长?


 1. 在直角三角形ABC中,斜边AB=1
1. 在直角三角形ABC中,斜边AB=1![]() ,则AB
,则AB![]() 的值是( )
的值是( )
A.2 B.4 C.6 D.8
2. 如图,学校有一块长方形花铺,有极少数人为了避开拐角走“捷径”,
在花铺内走出了一条“路”.他们仅仅少走了 ![]() 步路(假设2步为1米),
步路(假设2步为1米),
却踩伤了花草.
 3. 直角三角形两直角边长分别为5和12,则它斜边上的高为_______.
3. 直角三角形两直角边长分别为5和12,则它斜边上的高为_______.
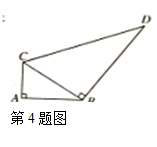
4 一个零件的形状如图所示,已知AC=3![]() ,AB=4
,AB=4![]() ,B
,B![]() D=12
D=12![]() 求CD的长.
求CD的长.
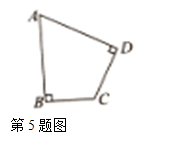
5. 如图所示,在四边形ABCD 中,∠A=60°,∠B=∠D=90°,BC=2,CD=3,求AB的长.
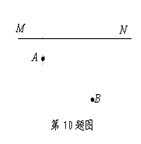
6. 如图,一个牧童在小河的南4km的A处牧马,而他正位于他的小屋B
的西8km北7km处,他想把他的马牵到小河边去饮水,然后回家.他要完成![]() 这件事情所走的最短路程是多少?
这件事情所走的最短路程是多少?
 7如图,某会展中心在会展期间准备将高5m,长1
7如图,某会展中心在会展期间准备将高5m,长1![]() 3m,宽2m的楼道上铺地毯
3m,宽2m的楼道上铺地毯
,已知地毯平方米18元,请你帮助计算一下,铺完这个楼道至少需要多少元钱?
通讯地址: 广州市天河区东圃黄村龙怡苑 (510660)邮箱:lzm6308@163.com 联系QQ:534386438
Copyright © 2008-2012 klxkc.com All Rights Reserved. 粤ICP备15026984号-1

