课案（学生用）

数据的波动（第四课时）

（课型：习题课）

【学习目标】

1.知识与技能

（1）理解方差的概念和计算公式的形成过程．

（2）掌握方差的计算公式并会应用方差比较两组数据波动的大小．

过程与方法

经历探索方差的应用过程，体会数据波动中方差的求法，积累统计经验，培养学生用统计的知识描述、分析数据，解决实际问题的能力．

情感、态度与价值观

培养学生统计意识，形成尊重事实、用数据说话的态度，认识数据处理的实际意义．

2.中考要求：掌握方差、标准差及其应用，掌握用样本方差估计总体方差．

3.根据学生能力发展水平的差异，明确本课教学的层次性目标，即针对优秀生、中等生、学困生三类学生的能力层级要求要有明显区分，要重点关注学困生；

4.充分了解学情，明确本课教学目标的针对性，做到有的放矢．

【学习重难点】

重点：理解极差、方差的概念，掌握其求法．

难点：应用方差对数据波动情况的比较，判断．

【课时安排】

一课时．

【学习过程设计】

课前延伸

知识回顾

1.描述一组数据的离散程度（即波动大小）的量：                                等．

2.极差：

（1）极差计算公式：                                                    ．

注意：极差越小，这组数据的离散程度（即波动大小）就越      ，这组数据就越           ．

（2）用极差来衡量一组数据的离散程度（即波动大小）的优缺点：（回忆）

3.方差（或标准差）：

  （1）方差计算公式：                                                         ；

       标准差计算公式：                                                       ．

注意：①方差的单位是                ；而标准差的单位是               ．

②方差（或标准差）越小，这组数据的离散程度（即波动大小）就越      ，这组数据就越            ．

             ③两组数据比较时，一组数据的极差大，这组数据的方差（或标准差）不一定就大！

（2）填表：

样本	平均数	方差	标准差
, ,，，，… ,
, ,… ,
, , ，，… ,
, ,… ,

（3）区分“二选一”和“对二者做出评价”这两类题型的回答的不同：（回忆）

 

课内探究

一、试试你的身手（每小题4分，共24分）

1．某校有人数相等的甲、乙两班，所有学生都参加了同一次数学测验，两班的平均分和方差分别为=82分，=82分，=245，=190．那么成绩较为整齐的是       班（填“甲”或“乙”）．

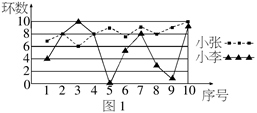
2．小张和小李去练习射击，第一轮10枪打完后两人的成绩如图1所示，通常新手的成绩不太稳定，那么根据图中的信息，估计小张和小李两人中新手是           ．

3．已知一个样本的方差，则此样本的平均数为          ．

4．某日天气预报说今天最高气温为8℃，气温的极差为10℃，则该日最低气温为       ．

5．已知一组数-1，x，0，1，-2的平均数是0，则这组数据的方差是         ．

6．设x1，x2，…，xn的平均数为x，方差为．若s2=0，则x1，x2，…，xn应满足的条件是     ．

二、相信你的选择（每小题3分，共18分）

1．人数相同的甲、乙两个团队在同一次比赛中，所得平均分和方差如下：80分，，，则成绩较为稳定的队是（    ）

A．乙队 B．甲队 C．两队成绩一样稳定 D．丁队

2．在统计中，样本的方差可以近似地反映总体的（    ）

A．平均状态 B．波动大小 C．分布规律 D．集中趋势

3．刘翔在出征奥运会前，刻苦进行110米跨栏训练，教练对他10次的训练成绩进行分析，判断他的成绩是否稳定，则教练需要知道刘翔这10次成绩的（    ）

A．众数 B．方差 C．平均数 D．频数

4．某次体育活动中，统计甲、乙两班学生每分钟跳绳的成绩（单位：次）情况如下表：

班级	参加人数	平均次数	中位数	方差
甲班	55	135	149	190
乙班	55	135	151	110

下面有三个命题：

①甲班学生的平均成绩高于乙班学生的平均成绩；

②甲班学生成绩的波动比乙班学生成绩的波动大；

③甲班学生成绩优秀的人数不多于乙班学生成绩优秀的人数（跳绳次数≥150次为优秀）．

则正确的命题是（    ）

A．① B．② C．③D．②③

5．一城市准备选购一千株高度大约为2m的某种风景树来进行街道绿化，有四个苗圃生产基地投标（单株树的价格都一样）．采购小组从四个苗圃中都任意抽查了20株树苗的高度，得到的数据如下：

	树苗平均高度（单位：m）	方差
甲苗圃	1.8	0.04
乙苗圃	1.8	0.36
丙苗圃	2.0	0.36
丁苗圃	2.0	0.04

请你帮采购小组出谋划策，应选购（    ）

A．甲苗圃的树苗 B．乙苗圃的树苗

C．丙苗圃的树苗 D．丁苗圃的树苗

6．已知样本数据为5，6，7，8，9，则它的方差为（    ）

A．10 B． C．2 D．

三、挑战你的技能（共40分）

1．(13分)某校八年级学生开展踢毽子比赛活动，每班派5名学生参加．按团体总分多少排列名次，在规定时间内每人踢100个以上(含100个)为优秀，下表是成绩最好的甲班和乙班5名学生的比赛数据(单位：个)．

	1号	2号	3号	4号	5号	总分
甲班	100	98	110	89	103	500
乙班	86	100	98	119	97	500

经统计发现两班总分相等，此时有学生建议，可通过考查数据中的其他信息作为参考．请你解答下列问题：

(1)计算甲、乙两班的优秀率．

(2)求两班比赛数据的中位数．

(3)计算两组比赛数据的方差?

(4)根据以上信息，你认为应该把冠军奖状发给哪一个班级?简述理由．

 

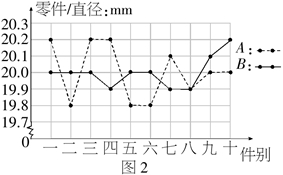
2．（13分）为选派一名学生参加全市实践活动技能竞赛，A、B两位同学在校实习基地现场进行加工直径为20mm的零件的测试，他俩加工的10个零件的相关数据如图2及下表所示（单位：mm）．

 

	平均数	方差	完全符合要求的个数
A	20	0.026	2
B	20		5

根据测试得到的有关数据，试解答下列问题：

（1）考虑平均数与完全符合要求的个数，你认为         的成绩好些．

（2）计算出的大小，考虑平均数与方差，说明谁的成绩好些．

（3）考虑图中折线走势及竞赛中加工零件个数远远超过10个的实际情况，你认为派谁去参赛较合适？说明你的理由．

 

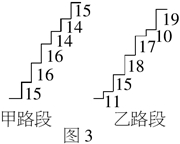
3．（14分）在某旅游景区上山的一条小路上，有一些断断续续的台阶，如图3是其中的甲、乙两段台阶的示意图．请你用所学过的有关统计的知识（平均数、中位数、方差和极差等）回答下列问题：

（1）两段台阶路有哪些相同点和不同点？

（2）哪段台阶路走起来更舒服？为什么？

（3）为方便游客行走，需要重新整修上山的小路．对于这两段台阶路，在台阶数不变的情况下，请你提出合理的整修建议．（图中的数字表示每一级台阶的高度，且台阶高度越均匀，走起来越舒服．）

 

四、拓广探索（18分）

现有A、B两个班级，每个班级各有45名学生参加一次测试，每名参加者可获得0，1，2，3，4，5，6，7，8，9分这几种不同的分值中的一种．测试结果A班的成绩如下表所示，B班的成绩如图4所示．

A班
分数	0	1	2	3	4	5	6	7	8	9
人数	1	3	5	7	6	8	6	4	3	2

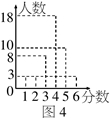(1)由图表可知，          班的方差较大；

(2)若两班合计共有60人及格，问参加者最少获           分才可以及格．

 

 

 

备用题

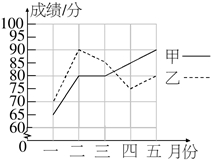
1．为了从甲、乙两名学生中选拔一人参加今年六月份的全省中学生数学竞赛，每个月要对他们的学习水平进行一次测验，如下图是两人赛前5次测验成绩的折线统计图．

（1）分别求出甲、乙两名学生赛前5次测验成绩的平均数、中位数及方差；

（2）如果你是他们的辅导教师，请制定两种不同的规则来评判甲、乙二人的成绩，并选派一名学生参加这次数学竞赛．

 

2．下表是某县统计局随机抽样调查甲、乙两个村10户居民2009年人均纯收入的情况．(单位:千元/人)

甲村被调查户人口数	3	5	4	3	4	5	4	4	3	3
乙村被调查户人口数	6	7	5	5	4	4	4	3	3	2
被调查户人均纯收入	0.9	1.2	1.3	1.4	1.5	1.6	1.8	2.0	2.2	2.4

由上表计算得甲村被调查户的人均纯收入≈1 608元，标准差s甲≈416.4，乙村被调查户的人均纯收入≈1 495元，标准差s乙≈411.4．已知该县2006年农民人均纯收入是1 490元，2006年全国农民人均纯收入是2 476元．

（1）根据样本估计这两个村平均每个家庭的人口数；

（2）以上数据说明什么问题，请你根据学过的统计知识，从不同角度加以解释．（注：标准差=）