| 上传:admin | 审核发布:admin | 更新时间:2015-3-23 15:19:39 | 点击次数:672次 |
|
教学时间 |
|
课题 |
26.2用函数的观点看一元二次方程(1) |
课型 |
新授课 |
|||||||
|
教 学 目 标 |
知 识 和 能 力 |
通过探索,使学生理解二次函数与一元二次方程、一元二次不等式之间的联系。 |
||||||||||
|
过 程 和 方 法 |
使学生能够运用二次函数及其图象、性质解决实际问题,提高学生用数学的意识。 |
|||||||||||
|
情 感 态 度 价值观 |
进一步培养学生综合解题能力,渗透数形结合思想。 |
|||||||||||
|
教学重点 |
使学生理解二次函数与一元二次方程、一元二次不等式之间的联系,能够运用二次函数及其图象、性质去解决实际问题 |
|||||||||||
|
教学难点 |
进一步培养学生综合解题能力,渗透数形结合的思想 |
|||||||||||
|
教学准备 |
教师 |
多媒体课件 |
学生 |
“五个一” |
||||||||
|
课 堂 教 学 程 序 设 计 |
设计意图 |
|||||||||||
|
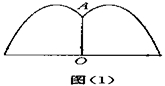
一、引言 在现实生活中,我们常常会遇到与二次函数及其图象有关的问题,如拱桥跨度、拱高计算等,利用二次函数的有关知识研究和解决这些问题,具有很现实的意义。本节课,请同学们共同研究,尝试解决以下几个问题。 二、探索问题 问题1:某公园要建造一个圆形的喷水池,在水池中央垂直于水面竖一根柱子,上面的A处安装一个喷头向外喷水。连喷头在内,柱高为0.8m。水流在各个方向上沿形状相同的抛物线路径落下,如图(1)所示。
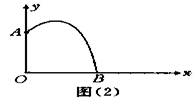
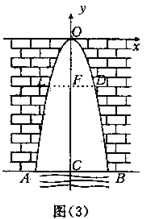
根据设计图纸已知:如图(2)中所示直角坐标系中,水流喷出的高度y(m)与水平距离x(m)之间的函数关系式是y=-x2+2x+5。 (1)喷出的水流距水平面的最大高度是多少? (2)如果不计其他的因素,那么水池至少为多少时,才能使喷出的水流都落在水池内? 教学要点 1.让学生讨论、交流,如何将文学语言转化为数学语言,得出问题(1)就是求函数y=-x2+2x+5最大值,问题(2)就是求如图(2)B点的横坐标; 2.学生解答,教师巡视指导; 3.让一两位同学板演,教师讲评。 问题2:一个涵洞成抛物线形,它的截面如图(3)所示,现测得,当水面宽AB=1.6m时,涵洞顶点与水面的距离为2.4m。这时,离开水面1.5m处,涵洞宽ED是多少?是否会超过1m?
1.教师分析:根据已知条件,要求ED的宽,只要求出FD的长度。在如图(3)的直角坐标系中,即只要求出D点的横坐标。因为点D在涵洞所成的抛物线上,又由已知条件可得到点D的纵坐标,所以利用抛物线的函数关系式可以进一步算出点D的横坐标。 2.让学生完成解答,教师巡视指导。 3.教师分析存在的问题,书写解答过程。 解:以AB的垂直平分线为y轴,以过点O的y轴的垂线为x轴,建立直角坐标系。 这时,涵洞的横截面所成抛物线的顶点在原点,对称轴为y轴,开口向下,所以可设它的 函数关系式为:y=ax2 (a<0) (1) 因为AB与y轴相交于C点,所以CB=2=0.8(m),又OC=2.4m,所以点B的坐标是(0.8,-2.4)。 因为点B在抛物线上,将它的坐标代人(1),得 -2.4=a×0.82 所以:a=-4 因此,函数关系式是 y=-4x2 (2) 。。。。。。。。。。。。。。。。。。。。
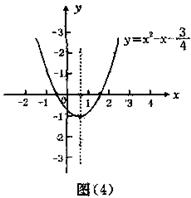
问题3:画出函数y=x2-x-3/4的图象,根据图象回答下列问题。 (1)图象与x轴交点的坐标是什么; (2)当x取何值时,y=0?这里x的取值与方程x2-x-4=0有什么关系? (3)你能从中得到什么启发? 教学要点 1.先让学生回顾函数y=ax2+bx+c图象的画法,按列表、描点、连线等步骤画出函数y=x2-x-4的图象。 2.教师巡视,与学生合作、交流。 3.教师讲评,并画出函数图象,如图(4)所示。 4.教师引导学生观察函数图象,回答(1)提出的问题,得到图象与x轴交点的坐标分别是(-2,0)和(2,0)。 5.让学生完成(2)的解答。教师巡视指导并讲评。
三、试一试 根据问题3的图象回答下列问题。 (1)当x取何值时,y<0?当x取何值时,y>0? (当-2<x<2时,y<0;当x<-2或x>2时,y>0) (2)能否用含有x的不等式来描述(1)中的问题? (能用含有x的不等式采描述(1)中的问题,即x2-x-4<0的解集是什么?x2-x-4>0的解集是什么?) 想一想:二次函数与一元二次不等式有什么关系? 让学生类比二次函数与一元二次不等式方程的关系,讨论、交流,达成共识: (1)从“形”的方面看,二次函数y=ax2+bJ+c在x轴上方的图象上的点的横坐标,即为一元二次不等式ax2+bx+c>0的解;在x轴下方的图象上的点的横坐标.即为一元二次不等式ax2+bx+c<0的解。 (2)从“数”的方面看,当二次函数y=ax2+bx+c的函数值大于0时,相应的自变量的值即为一元二次不等式ax2+bx+c>0的解;当二次函数y=ax2+bx+c的函数值小于0时,相应的自变量的值即为一元二次不等式ax2+bc+c<0的解。这一结论反映了二次函数与一元二次不等式的关系。 四、小结: 1.通过本节课的学习,你有什么收获?有什么困惑? 2.若二次函数y=ax2+bx+c的图象与x轴无交点,试说明,元二次方程ax2+bx+c=0和一元二次不等式ax2+bx+c>0、ax2+bx+c<0的解的情况。 |
|
|||||||||||
|
作业 设计 |
必做 |
教科书P19:1、2 |
||||||||||
|
选做 |
教科书P20:5 |
|||||||||||
|
教学 反思 |
|
|||||||||||
通讯地址: 广州市天河区东圃黄村龙怡苑 (510660)邮箱:lzm6308@163.com 联系QQ:534386438
Copyright © 2008-2012 klxkc.com All Rights Reserved. 粤ICP备15026984号-1