| 上传:admin | 审核发布:admin | 更新时间:2015-3-23 15:21:40 | 点击次数:659次 |
26.2用函数观点看待一元二次方程
年级:九年级 科目:数学 课型:新授 主备:徐中国 审核:姜艳 薛柏双 田娟
备课时间:2010.11.15 上课时间:2010.11.19
学习目标:
1.探索二次函数与一元二次方程、一元二次不等式之间的关系.
2.掌握一元二次方程(组)的图象解法.
重点、难点
1.重点:探索二次函数与一元二次方程、一元二次不等式之间的关系.
2.难点:掌握一元二次方程(组)的图象解法.
导学过程:阅读教材P16 — 19 , 完成课前预习
【课前预习】
1:准备知识
(1) 一元二次方程根的情况:
(2)一次函数与一元一次方程的关系:
2:探究1
以40米/秒的速度将小球沿与地面成300角的方向击出时,球的飞行路线将是一条抛物线。如果不考虑空气阻力,球的飞行高度h米与飞行时间t秒之间具有关系![]() 。考虑以下问题:
。考虑以下问题:
(1) 球的飞行高度能否达到15米?如能,需要多少飞行时间?
(2) 球的飞行高度能否达到20米?如能,需要多少飞行时间?
(3) 球的飞行高度能否达到20.5米?为什么?
(4) 球从飞出到落地需要用多少时间?
探究2给出三个二次函数:(1)![]() ;(2)
;(2)![]() ;
;
(3)![]() .它们的图象分别为
.它们的图象分别为
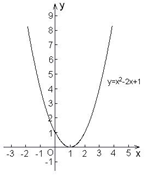

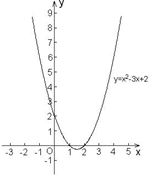
观察图象与x轴的交点个数,分别是 个、 个、 个.你知道图象与x轴的交点个数与什么有关吗?
另外,能否利用二次函数![]() 的图象寻找方程
的图象寻找方程![]() ,不等式
,不等式![]() 或
或![]() 的解?
的解?
3:结论
一般的,从二次函数![]() 的图象可知,
的图象可知,
(1) 如果抛物线![]() 与x轴有公共点,公共点的横坐标是x0,那么当x= 时,函数的值是0,因此x= 就是方程
与x轴有公共点,公共点的横坐标是x0,那么当x= 时,函数的值是0,因此x= 就是方程![]() 的一个根。
的一个根。
(2) 二次函数的图象与x轴的位置关系有三种:没有公共点,有一个公共点,有两个公共点。这对应着一元二次方程根的三种情况: 实数根,有 的实数根,有 的实数根。
【课堂活动】
活动1:预习反馈
活动2:典型例题
例1.画出函数![]() 的图象,根据图象回答下列问题.
的图象,根据图象回答下列问题.
(1)图象与x轴、y轴的交点坐标分别是什么?
(2)当x取何值时,y=0?这里x的取值与方程![]() 有什么关系?
有什么关系?
(3)x取什么值时,函数值y>0?x取什么值时,函数值y<0?
例2.(1)已知抛物线![]() ,当k= 时,抛物线与x轴相交于两点.
,当k= 时,抛物线与x轴相交于两点.
(2)已知二次函数![]() 的图象的最低点在x轴上,则a= .
的图象的最低点在x轴上,则a= .
(3)已知抛物线![]() 与x轴交于两点A(α,0),B(β,0),且
与x轴交于两点A(α,0),B(β,0),且![]() ,则k的值是 .
,则k的值是 .
例3.利用函数的图象,求下列方程(组)的解:
(1) ![]() ; (2)
; (2)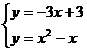
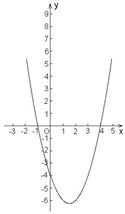 活动3:随堂训练
活动3:随堂训练
1.已知二次函数![]() 的图象如图,
的图象如图,
则方程![]() 的解是 ,
的解是 ,
不等式![]() 的解集是 ,
的解集是 ,
不等式![]() 的解集是 .
的解集是 .
2.抛物线![]() 与y轴的交点坐标为 ,与x轴的交点坐标为 .
与y轴的交点坐标为 ,与x轴的交点坐标为 .
3.已知方程![]() 的两根是
的两根是![]() ,-1,则二次函数
,-1,则二次函数![]() 与x轴的两个交点间的距离为 .
与x轴的两个交点间的距离为 .
4.不论自变量x取什么数,二次函数![]() 的函数值总是正值,则m的取值范围为
的函数值总是正值,则m的取值范围为
活动4:课堂小结
【课后巩固】
1.已知二次函数![]() ,画出此抛物线的图象,根据图象回答下列问题.
,画出此抛物线的图象,根据图象回答下列问题.
(1)方程![]() 的解是什么?
的解是什么?
(2)x取什么值时,函数值大于0?x取什么值时,函数值小于0?
2.已知二次函数![]() ,
,
求:(1)此函数图象的开口方向、对称轴和顶点坐标,并画出草图;
(2)以此函数图象与x轴、y轴的交点为顶点的三角形面积;
(3)x为何值时,y>0.
3.已知二次函数![]() ,
,
(1)试说明:不论m取任何实数,这个二次函数的图象必与x轴有两个交点;
(2)m为何值时,这两个交点都在原点的左侧?
(3)m为何值时,这个二次函数的图象的对称轴是y轴?
4.你能否画出适当的函数图象,求方程![]() 的解?
的解?
通讯地址: 广州市天河区东圃黄村龙怡苑 (510660)邮箱:lzm6308@163.com 联系QQ:534386438
Copyright © 2008-2012 klxkc.com All Rights Reserved. 粤ICP备15026984号-1

