| 上传:admin | 审核发布:admin | 更新时间:2015-3-23 15:22:43 | 点击次数:761次 |
一·自主学习目标
1、 掌握二次函数与一元二次方程之间的关系,会根据二次函数的![]()
图像知道二次函数与x轴的交点情况同一元二次方程的根的情况之间的关系
2、
![]()
![]()
二、学习重难点:
重点:二次函数与一元二次方程之间的关系
难点:会根据二次函数的图像知道二次函数与x轴的交点情况同一元二![]() 次方程的根的情况
次方程的根的情况
三、导学过程:
(一)旧知回顾
二次函数的![]() 的图象如图所示。根据图
的图象如图所示。根据图![]() 象回答:
象回答:
⑴![]() 为何值时,
为何值时, ![]() ?
?
⑵ 你能根据图象,求方程![]() 的根吗?
的根吗?
⑶ 二次函数![]() 与方程
与方程![]() 之间有何关系
之间有何关系
(二)新知探究
1、二次函数与一元二次方程之间的关系
【探究】教材P16问题:如图26-2-2,以40m/s的速度将小球沿与地面成30![]() °角的方向击出时,球的飞行路线将是一条抛物线。如果不考虑空气阻力,球的飞行高度
°角的方向击出时,球的飞行路线将是一条抛物线。如果不考虑空气阻力,球的飞行高度![]() (单位:m)与飞行时间
(单位:m)与飞行时间![]() (单位:s)之间具有关系:
(单位:s)之间具有关系:![]() 。
。
考虑以下问题
⑴ 球的飞行高度能否达到15m?如能,需要多少飞行时间?
⑵ 球的飞行高度能否达到20m?如能,需要多少飞行时间?
考虑以下问题:
⑴ ![]() 球的飞行高度能否达到
球的飞行高度能否达到![]() 15m?如能,需要多少飞行时间?
15m?如能,需要多少飞行时间?
⑵ 球的飞行高度能否达到20m?如能,需要多少飞行时间?
⑶ 球的飞行高度能否达到20.5m?为什么?
⑶ 球的飞行高度能否达到20.5m?为什么?[来源:Z|xx|k.Com]
⑷ 球从飞出到落地需要多少时间?
[来源:学科网ZXXK]
。

[来源:学科网ZXXK]
【归纳】二次函数与一元二次方程有如下关系:二次函数与一元二次方程之间有如下关系①函数![]() ,当函数值
,当函数值![]() 为某一确定值
为某一确定值![]() 时,对应自变量
时,对应自变量![]() 的值就是方程
的值就是方程![]() 的根.②特别是
的根.②特别是![]() 时,对应自变量x的值就是方程
时,对应自变量x的值就是方程![]() 的根。以上关系,反过来也成立。
的根。以上关系,反过来也成立。
【思考】利用以上关系,可以解决什么问题
2. ![]() 二次函数的图象与x轴的交点情况同一元二次方程的根的情况之间的关系
二次函数的图象与x轴的交点情况同一元二次方程的根的情况之间的关系
【探究】观察图26-2-3中的抛物线与x轴的交点情况,你能得出相应方程的根吗?
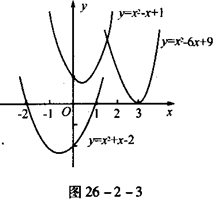 ⑴ 方程x2+x-2=0的根是
⑴ 方程x2+x-2=0的根是
⑵ 方程x2-6![]() x+9=0的根是
x+9=0的根是
⑶ 方程x2![]() -x+1=0 [来源:学|科|网Z|X|X|K]
-x+1=0 [来源:学|科|网Z|X|X|K]
【归纳】一般地,从二次函数![]() 的图象可知:
的图象可知:
⑴ 如果抛物线![]() 与x轴有公共点(x0,0),那么 就是方程
与x轴有公共点(x0,0),那么 就是方程![]() 的一个根。
的一个根。
⑵ 抛物线与x轴的三种位置关系:没有公共点,有一个公共点,有两个公共点。这对应着一元二次方程根的三种情况:没有实数根,有两个相![]() 等的实数根,有两个不等的实数根。
等的实数根,有两个不等的实数根。
学 ![]()
三 ( 三 )合作探究[来源:学+科+网]
1、
⑵ 抛物线与x轴的三种位置关系:没有公共点,有一个公共点,有两个公共点。这对应着一元二次方程根的三种情况:没有实数根,有两个相等的实数根,有两个不等的实数根。
三、合作探究,应用迁移
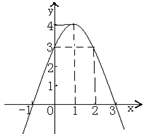
例1、如图,是二次函数y=-x2+2x+3的图象,你能看出哪些方程的根?
通讯地址: 广州市天河区东圃黄村龙怡苑 (510660)邮箱:lzm6308@163.com 联系QQ:534386438
Copyright © 2008-2012 klxkc.com All Rights Reserved. 粤ICP备15026984号-1

