课题  27.3  位  似 2 学案 人教版九年级下   　

      

导学目标知识点：掌握位似图形在直角坐标系下的点的坐标的变化规律

                  能利用直角坐标系下位似图形对应点坐标变化的规律来解决问题

课    时：1课时

导学方法：整理、分析、归纳法

导学过程：

一、自主探究（课前导学）

 1．如图，△ABC三个顶点坐标分别为A(2,3)，B(2,1)，C(6,2).

（1）将△ABC向左平移三个单位得到△A1B1C1，写出A1、B1、C1三点的坐标；

（2）写出△ABC关于x轴对称的△A2B2C2三个顶点A2、B2、C2的坐标；

（3）将△ABC绕点O旋转180°得到△A3B3C3，写出A3、B3、C3三点的坐标．

2、在平面直角坐标系中有两点A（6，3），B（6，0），以原点O为位似中心，相似比为，把线段AB缩小

方法一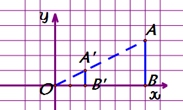：  方法二：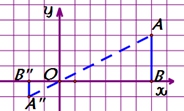

 

探究：（1）在方法一中，的坐标是        ，的坐标是        ，对应点坐标之比是　　　；（2）在方法二中，的坐标是        ，的坐标是        ，对应点坐标之比是　　　

二、合作探究（课堂导学）

实验探究1：如图，三个顶点坐标分别为，以点为位似中心，相似比为２，将放大，观察对应顶点坐标的变化，你有什么发现？

   位似变换后的对应点坐标为：                            

 

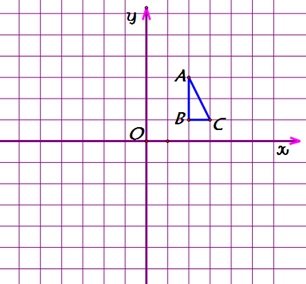
归纳：在平面直角坐标系中，如果位似变换是以原点为位似中心，相似比为，那么位似图形对应点的坐标的比等于         ；

实验探究2：如图，在平面直角坐标系中，四边形ABCD的坐标分别为A（-6,6），B（-8,2），C(-4,0)D（-2,4）画出一个以原点O为位似中心，相似比为1：2的位似图形。

 

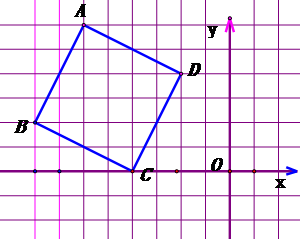
三、讨论交流（展示点评）

四、课堂检测（当堂训练）

如图，在12×12的正方形网格中，△TAB的顶点坐标分别为T（1，1）、A（2，3）、B（4，2）．

（1）以点T（1，1）为位似中心，按比例尺TA′∶TA=3∶1在位似中心的同侧将△TAB放大为△TA′B′，放大后点A、B的对应点分别为A′、B′．画出△TA′B′，并写出点A′、B′的坐标；

 

 

 

 

（2）在（1）中，若C（a，b）为线段AB上任一点，写出变化后点C的对应点C′的坐标．

 

 

 

 

 

拓展延伸（课外练习）：

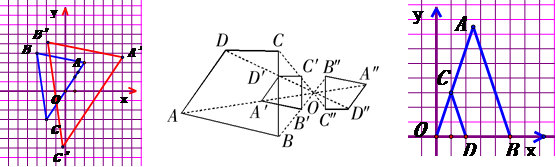
1、如图，与是位似图形，且顶点都在格点上，则位似中心的坐标是_______

2、如图，四边形ABCD和四边形A′B′C′D′位似，位似比，四边形A′B′C′D′和四边形A″B″C″D″位似，位似比．四边形A″B″C″D″和四边形ABCD是位似图形吗？位似比是多少？

 

 

 

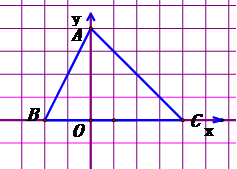
3、如图表示△AOB和把它缩小后得到的△COD，求△COD和△AOB的相似比．

 

 

4、如图，△ABC三个顶点坐标分别为A（2，－2），B（4，－5），C（5，－1），以原点O为位似中心，将这个三角形放大为原来的2倍．

 

 

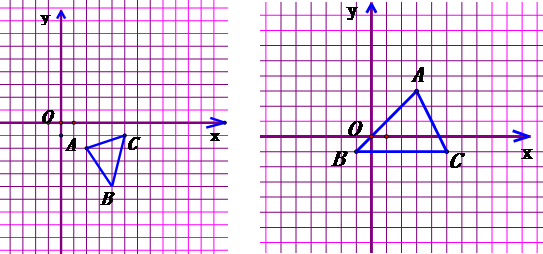
5、如图，△ABC是格点三角形．在建立平面直角坐标系后，点B的坐标为（-1，-1）．

(1)把△ABC向左平移5格后得到△A1B1C1，则点B1的坐标为____________

(2)把△ABC绕点C按顺时针方向旋转90o后得到△A2B2C，则点B2的坐标为___________

(3)把△ABC以点A为位似中心放大，使放大前后对应边长的比为1：2，则B3的坐标是_______

 

 

6.如图，每个小正方形边长均为1，点O和△ABC的顶点均在小正方形的顶点.

（1）以O为位似中心，在网格图中作△A′B′C′和△ABC位似，且位似比为1︰2；

（2）连接（1）中的AA′,求四边形AA′C′C的周长.（结果保留根号）