| 上传:admin | 审核发布:admin | 更新时间:2015-3-29 9:31:27 | 点击次数:774次 |
湖南省邵阳市隆回县第二中学高中数学 空间几何体的结构导学案 新人教A版必修2
【学习目标】
1. 通过观察模型、图片,使学生理解并能归纳出棱柱、棱锥、棱台的结构特征。
2. 通过对棱柱、棱![]() 锥、棱台的观察分析,培养学生的观察能力、空间想象能力和抽象概括能力。
锥、棱台的观察分析,培养学生的观察能力、空间想象能力和抽象概括能力。
3. 通过教学活动,逐步培养学生探索问题的精神。
【自主学习】
任务一
阅读教材第2~3页,回答下列问题:
1. 空间几何体:____________________________________________________ 。
2. 什么是多面体、多面体的面、棱、顶点?
3. 什么是旋转体、旋转体的轴?
任务二
阅读教材第3~4页,回答下列问题:
1.什么是棱柱、棱柱的底、侧面、侧棱、顶点?有什么特征?如何表示?如何分类?
思考:正方体、长方体是棱![]() 柱吗?
柱吗?
2.什么是棱锥、棱锥的底、侧面、侧棱、顶点?有什么特征?如何表示?如何分类?
思考:有一个面是多边形,其余各面是三角形的多面体是棱锥吗?
3.什么是棱台、棱台的底、侧面、侧棱、顶点?有什么特征?如何表示?如何分类?
【合作探究】
1.棱柱、棱锥、棱台都是多面体,当底面发生变化时,它们能否互相转化呢?
【目标检测】
A级:必做题
1.一个多面体至少有________个面,面数最少的棱柱有_________个顶点。
2.在三棱锥A-BCD,可以当作棱锥底面的三角形的个数为( )
A.1 B.2 C.3 D.4
3.在棱柱中( )
A、只有两个面平行 B、所有的棱都平行
C、所有的面都是平行四边形 D、两底面平行,且各侧棱也互相平行
4.棱台不具有的性质是( )
A.两底面平行且相似 B.侧面都是梯形 C.侧棱都平行 D.侧棱延长后必交于一点
B级:选做题
1、若一个棱锥的侧面都是等边三角形,这个棱锥最多是( )棱锥。
A、6 B、 5 C、 4 D、 3
2、下列三个命题:
(1)用一个平面去截棱锥,棱锥底面和截面之间的部分是棱台;
(2)两个面平行且相似,其余各面都是梯形的多面体是棱台;
(3)有两个面互相平行,其余四个面都是等腰梯形的六面体是棱台。
其中正确的有( )
A、0个 B、 1个 C、 2个 D、3个
※ 知识拓展
1.平行六面体:底面是平行四边形的四棱柱。
2.直棱柱:侧棱垂直于底面的棱柱。
3.正棱柱:底面是正多边形的直棱柱。
4.正棱锥:底面是正多边形,并且顶点在底面的射影是底面正多边形的中心的棱锥。
5.正棱台:由正棱锥截得的棱台。
|
※ 自我评价 你完成本节导学案的情况为( ). A. 很好 B. 较好 C. 一般 D. 较差
|
高一数学 必修2 编制:廖信山 审核:王育仁 使用时间:2013年11月___日
班级:__________ 组别:_________ 组号:_________ 姓名:___________
空间几何体的结构(2)
【学习目标】
1.通过观察模型、图片,使学生理解并能归纳出圆柱、圆锥、圆台、球的结构特征。
2.理解由柱、锥、台、球组成的简单组合体的结构特征,并能描述这些几何体的结构特征。
3.进一步培养从现实生活中的物体进行抽象、概括的能力及观察、分析、类比的能力。
【自主学习】
任务一 阅读教材第5~6页,回答下列问题:
1.什么是圆柱、圆柱的轴、底面、侧面、母线?有什么特征?如何表示?
2.什么是圆锥、圆锥的轴、底面、侧面、母线?有什么特征?如何表示?
3.什么是圆台、圆台的轴、底面、侧面、母线?有什么特征?如何表示?
4.什么是球、球的球心、半径、直径?
任务二 阅读教材第6~7页,回答下列问题:
什么是简单组合体?简单组合体有哪些基本形式?
【合作探究】
1.圆柱、圆锥、球都是由平面图形旋转得到的,圆台可以由什么平面图形旋转得到?如何旋转?
【目标检测】
A级:必做题
1.用一个平面去截一个几何体,各个截面都是圆,则这个几何体一定是( )
A.圆柱 B.圆锥 C.圆台 D.球
2.将一个等腰梯形绕着它的较长的底边所在的直线旋转一周,所得的几何体包括( )
A.一个圆台和两个圆锥 ![]() B. 一个圆台和两个圆柱
B. 一个圆台和两个圆柱
C.一个圆柱和两个圆台 D. 一个圆柱和两个圆锥
3.下列说法中不正确的是( )
A.圆柱的侧面展开图是一个矩形 B.直角三角形绕它的一边旋转一周形成的几何体是圆锥。
C. ![]() 圆台中平行于底面的截面是圆 D.圆锥中过轴的截面是一个等腰三角形
圆台中平行于底面的截面是圆 D.圆锥中过轴的截面是一个等腰三角形
4.画出一个直角三角形绕斜边所在的直线旋转一周得到的几何体,说说它的构成是怎样的?
B级:选做题
1、下列说法中错误的是( )
A.球的截面是圆 B. 球面上任何一点到球心的距离都相等
C.以半圆的直径所在直线为轴,半圆面旋转一周所得的几何体叫做球
D.以半圆的直径所在直线为轴,半圆旋转一周所得的曲面叫做球
2、下列命题,正确的是( )
A.圆锥的侧面展开图为扇形,这个扇形所在圆的半径等于圆锥的底面圆的半径
B.在圆柱的上、下底面的圆周上各取一点,则这两点的连线是圆柱的母线
C.在圆台上、下底面圆周上各取一点,则这两点的连线是圆台的母线
D.圆柱的任意两条母线所在的直线是互相平行的。
|
※ 自我评价 你完成本节导学案的情况为( ). A. 很好 B. 较好 C. 一般 D. 较差
|
高一数学 必修2 编制:廖信山 审核:王育仁 使用时间:2013年11月___日
班级:__________ 组别:_________ 组号:_________ 姓名:___________
空间几何体的三视图和直观图(1)
【学习目标】
1.了解空间几何体的表示形式:中心投影、平行投影、三视图。
2.理解几何体与三视图的关系,能画出简单几何体(长方体、棱柱、圆柱、圆锥、球等)及简单组合体的三视图。
3.能根据几何体的三视图还原其实物图。
【自主学习】
任务一 阅读教材第11~12页,完成下列填空:
1.投影的定义:由于光的照射,在__________物体后面的屏幕上可以留下这个物体的__________这种现象叫做投影。其中,___________叫做投影线,留下物体影子的__________叫做投影面。
2.投影的分类:
(1)中心投影:光由__________向外散射形成的投影,叫做中心投影,中心投影的投影线___________________。
(2)平行投影:在一束__________光线照射下形成的投影,叫做平行投影,平行投影的投影线_____________。在平行投影中,投影线_____________投影面时,叫做正投影,否则叫做________________。
想一想:当三角形ABC所在的平面与投影面平行时,三角形ABC的中心投影与三角形ABC有什么关系?三角形ABC的平行投影与三角形ABC有什么关系?
任务二 阅读教材第12~14页,完成下列填空:
1.几何体的三视图包括
(1)正视图:光线从几何体的_____面向_____面_____投影,得到的投影图,反映几何体的____________________。
(2)侧视图:光线从几何体的_____面向_____面_____投影,得到的投影图,反映几何体的____________________。
(3)俯视图:光线从几何体的_____面向_____面_____投影,得到的投影图,反映几何体的____________________。
2.三视图的画法要求:
(1)一般,____________在正视图的右边,____________在正视图的正下方。
(2)一个几何体的侧视图和正视图___________一样,俯视图和正视图___________一样,侧视图和俯视图___________一样,即“___________、___________、___________ ”。
(3)画几何体的三视图时,能看见的轮廓线和棱用__________表示,不能看见的轮廓线和棱用__________表示。
【合作探究】
1.画出圆台的三视图:
【目标检测】
A级:必做题
1、一图形的投影是一条线段,这个图形不可能是( )
A、线段 B、 直线 C 、圆 D 、梯![]() 形
形
2、一个几何体的某一个方向的视图是圆,则它不可能是( )
A、球体 B、圆锥 C、圆柱 D、长方体
3、下列几何体中,正视图、侧视图、俯视图相同的几何体是( )
A、球和圆柱 B、圆柱和圆锥 C、正方体和圆柱 D、球和正方体
4![]() 、一个含有圆柱、圆锥、圆台和球的简单组合体的三视图中一定含有( )
、一个含有圆柱、圆锥、圆台和球的简单组合体的三视图中一定含有( )
A、四边形 B、三角形 C、圆 D、椭圆
B级:选做题
1、下列命题中,正确的是( )
A、如果一个几何体的三视图是完全相同的,则这个几何体是正方形
B、如果一个几何体的正视图和俯视图都是矩形,则这个几何体是长方体
C、如果一个几何体的三视图都是矩形,则这个几何体是长方体
D、如果一个几何体的正视图和俯视图都是等腰梯形,则这个几何体是圆台
2、甲、乙、丙、丁四人分别面对面坐在一个四边形的桌子旁边,桌上一张纸上写着数字“9”,甲说他看到的是“6”,乙说他看到的是“![]() ”,丙说他看到的是“
”,丙说他看到的是“ ![]() ”,丁说他看到的是“
”,丁说他看到的是“ ![]() ”。则下列说法正确的是( )
”。则下列说法正确的是( )
A、甲在丁的对面,乙在甲的左边,丙在丁的右边
B、丙在乙的对面,丙的左边是甲,丙的右边是丁
C、甲在乙的对面,甲的右边是丙,丙的左边是丁
D、甲在丁的对面,乙在甲的右边,丙在丁的右边
|
※ 自我评价 你完成本节导学案的情况为( ). A. 很好 B. 较好 C. 一般 D. 较差
|
高一数学 必修2 编制:廖信山 审核:王育仁 使用时间:2013年11月___日
班级:__________ 组别:_________ 组号:_________ 姓名:___________
空间几何体的三视图和直观图(2)
【学习目标】
1.掌握斜二测画法及步骤,能用斜二测画法画一些简单平面图形和立体图形的直观图。
2.能根据直观图还原出原来的图形,培养学生的空间想象能力。
3.会将空间图形的三视图和直观图相互转化,养成举一反三的学习习惯。
【自主学习】
阅读教材第16~18页,完成下列填空:
1.水平放置的平面图![]() 形的斜二测画法基本步骤:
形的斜二测画法基本步骤:
(1)在已知图形中取_______________的x轴![]() 和y轴,两轴相交于点O,画直观图时,把它
和y轴,两轴相交于点O,画直观图时,把它
们画成对应的_______________,两轴交于_________,且使________________________,它
们确定的___________表示水平面。
(2)已知图形中平行于x轴或y轴的线段,在直观图中分别画成____________________
的线段。
(3)已知图形中平行于x轴的线段,在直观图中长度__________,平行于y轴的线段,在
直观图中长![]() 度___________________。
度___________________。
试一试:画出以下水平放置的直角三角形ABC的直观图。
 A
A
B C
2.画空间图形的直观图时,只需增加一个竖直的_____轴,且使____________________,并
把竖直的线段画成____________________,长度____________
试一试:画出棱长为4cm的正方体的直观图。
【合作探究】
任务一:如下图所示,梯形A/B/C/D/是水平放置的平面图形ABCD的直观图,若A/D/∥O/y/,A/B/∥C/D/, A/B/=![]() C/D/=2,A/D/=O/D/=1.请画出原来的平面几何图形,并求原图形的面积。
C/D/=2,A/D/=O/D/=1.请画出原来的平面几何图形,并求原图形的面积。
任务二:探究平面图形直观图的面积与原图形的面积有何关系?
【目标检测】
A级:必做题
1.利用斜二测画法画直观图时,下列说法正确的是( )
A、三角形的直观图是三角形 B、平行四边形的直观图是平行四![]() 边形;
边形;
C、正方形的直观图是正方形 D、菱形的直观图是菱形。
2.在原来的图形中,两条线段平行且相等,则在直观图中对应的两条线段( )
A、平行且相等 B、平行但不相等 C、相等但不平行 D、既不平行也不相等
3、下列说法中正确的是( )
A、互相垂直的两条直线的直观图仍然是互相垂直的直线 B、矩形的直观图可能是梯形
C、梯形的直观图可能是平行四边形 D、正方形的直观图可能是平行四边形
4、下列说法中正确的是( )
A、两条相交直线的直观图可能平行 B、两条平行直线的直观图可能相交
C、角的水平放置直观图一定是角 D、相等的角在直观![]() 图中仍然相等
图中仍然相等
B级:选做题
1、已知一个平面图形的直观图是边长为a的等边三角形,则原平面图形的面积是____________。
2、.已知一个几何体的三视图如下,请画出原几何体的直观图。

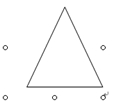

|
※ 自我评价 你完成本节导学案的情况为( ). A. 很好 B. 较好 C. 一般 D. 较差
|
高一数学 必修2 编制:廖![]() 信山 审核:王育仁 使用时间:2013年11月___日
信山 审核:王育仁 使用时间:2013年11月___日
班级:__________ 组别:_________ 组号:_________ 姓名:___________
空间几何体的表面积与体积(1)
【学习目标】
1.通过对柱、锥、台的研究,掌握柱、椎、台的侧面积和表面积公式。
2.能利用柱、椎、台的表面积公式进行计算和解决有关实际问题。
3.掌握一些简单组合体的表面积的计算方法,培养学生的空间想象能力和思维能力。
【自主学习】
任务一 阅读教材第23~24页,完成下列填空:
1.棱柱、棱锥、棱台的表面积、侧面积:
棱柱、棱锥、棱台是由多个平面图形围成的多面体,它们的表面积就是________________________,也就是________________________;它们的侧面积就是________________________。
2.(1)一个三棱柱的底面是直角三角形,两直角边分别是6、8,侧棱与底面垂直,侧棱长为6,则它的侧面积是_______________,表面积是_______________。
(2)棱长都为a的四面体的表面积![]() 是_______________。
是_______________。
任务二 阅读教材第24~25页,完成下列表格:
|
|
侧面展开图 |
侧面积公式 |
表面积公式 |
|
圆柱
|
|
|
|
|
圆锥
|
|
|
|
|
圆台
|
|
|
|
想一想:圆柱、圆锥、圆台的表面积公式有何联系?
【合作探究】
研究教材25页例2。
【目标检测】
A级:必做题
1.用长为4cm,宽为2cm的矩形做面围成一个圆柱,则此圆柱的侧面积为_____________.
2.长方体的过一个顶点的三条棱长的比是1:2:3,对角线的长是![]() ,则它的体积是_____。
,则它的体积是_____。
3.圆台的一个底面周长是另一个底面周长的3倍,母线长为3,圆台的侧面积为84,则圆台较小底面的半径为______。
4.已知圆锥的表面积为a m2,且它的侧面展开图是一个半圆,求这个圆锥的底面直径。
B级:选做题
1.四面体A-BCD四个面的重心分别为E,F,G,H,则四面体E-FGH的表面积与四面体A-BCD的表面积的比值是______。
2.在棱长为4cm的正方体ABCD-A1B1C1D1木块上,有一只蚂蚁从顶点A沿着表面爬行到顶点C1,求蚂蚁爬行的最短距离。
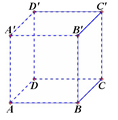
|
※ 自我评价 你完成本节导学案的情况为( ). A. 很好 B. 较好 C. 一般 D. 较差
|
高一数学 必修2 编制:廖信山 审核:王育仁 使用时间:2013年11月___日
班级:__________ 组别:_________ 组号:_________ 姓名:___________
空间几何体的表面积与体积(2)
【学习目标】
1.掌握柱、椎、台的体积公式以及球的体积和表面积公式。
2.能利用公式进行计算和解决有关实际问题。
3.掌握一些简单组合体的体积的计算方法,培养学生的空间想象能力和思维能力。
【自主学习】
1.回顾已学知识:
(1)棱长为a的正方体的体积公式是V=_________________。
(2)长、宽、高分别是a、b、c的长方体的体积公式是V=_________________。
(3)底面半径是r,高是h的圆柱的体积公式是V=_________________。
思考:它们的公式可以统一吗?
2.柱体、锥体、台体的体积公式:
阅读教材第25~26页,完成下列表格:
|
|
体积公式 |
|
柱体 |
|
|
锥体 |
|
|
台体 |
|
想一想:柱体、锥体、台体的体积有何联系?
3.球的体积和表面积公式:
|
|
体积公式 |
表面积公式 |
|
球 |
|
|
4.若圆柱、圆锥的底面![]() 直径和高都等于球的直径,则圆柱、圆锥、球的体积的比为_________________。
直径和高都等于球的直径,则圆柱、圆锥、球的体积的比为_________________。
【合作探究】
1.根据下列几何体的三视图,求几何体的体积:
正视图 侧视图 正视图 侧视图







俯视图 俯视图


(1) (2)
【目标检测】
A级:必做题
1.将一个气球的![]() 半径扩大1倍,它的体积扩大到原来的______倍.
半径扩大1倍,它的体积扩大到原来的______倍.
2.长方体的过一个顶点的三条棱的长分别是3、4、5,且它的八个顶点都在同一个球面上,则这个球的表面积是________________。
3.两个半径为1的铁球,熔化成一个大球,这个大球的半径为______。
4.半径为R的半圆卷成一个圆锥,则它的体积为_____________。
B级:选做题
1.用一个平面截一球得到直径为6cm的圆面,球心到这个平面的距离为4cm,球的体积是多少?
2.已知过球面上A、B、C三点的截面和球心的距离刚好等于球的半径的一半,且AB=BC=CA=2cm,求球的表面积。
|
※ 自我评价 你完成本节导学案的情况为( ). A. 很好 B. 较好 C. 一般 D. 较差
|
通讯地址: 广州市天河区东圃黄村龙怡苑 (510660)邮箱:lzm6308@163.com 联系QQ:534386438
Copyright © 2008-2012 klxkc.com All Rights Reserved. 粤ICP备15026984号-1

