3.3.3《直线的交点坐标与距离公式》习题课

【学习目标】

知识与技能：掌握解方程组的方法，求两条相交直线的交点坐标。掌握两点间距离公式，点到直线距离公式，会求两条平行直线间的距离。 

过程与方法：利用数形结合，结合思维变式对学生培养方法选择能力

情感态度与价值观：(1)培养学生观察、探索能力，运用数学语言表达能力，数学交流与评价能力．

(2)进一步理解数形结合思想，培养树立辩证统一的观点，培养形成严谨的科学态度和求简的数学精神．

【重点难点】

学习重点：直线的交点求法及距离公式的应用

学习难点：综合应用以及思想渗透

【学法指导】

1、重审教材，形成知识脉络。2、将直线的交点坐标与距离公式习部分曾做过的学案自己易忘、易出错的知识点和疑难问题以及解题方法规律，按照本习题课的要求进行重整。3、加强自主学习、审慎合作探究、着重能力提升。

【知识链接】

1、如果已知平面上两点P1(x1,y1)、P2(x2,y2), 

2、两相交直线的交点的坐标

3、点P(x0,y0)到直线Ax+By+C=0(A、B不同时为0)的距离为

4、已知两条平行线l1：Ax+By+C1=0, l2：Ax+By+C2=0(C1=C2).则l1与l2之间的距离为：

【学习过程】

基本类型问题概要

题型一：两点间距离公式的运用

已知三角形的顶点A（-1，5）B（-2，-1）C（4，7）求BC边上的中线长。

 

 

 

题型二：点到直线距离的应用

求过点P（-1，2）且与点A（2，3）和B（-4，5）距离相等的直线l的方程。

 

 

 

 

题型三：对称问题  求直线y=-4x+1关于点M（2，3）对称的直线方程。

 

 

 

 

 

题型四：直线方程的应用

求经过直线l₁：3x+2y-1=0和l₂：5x+2y+1=0的交点，且垂直于直线l₃：3x-5y+6=0的直线l的方程。

 

 

 

 

 

 

 

题型五：直线过定点问题及应用

1由“y-y0=k(x-x0)”求定点

把含有参数的直线方程改写成y-y0=k(x-x0)的形式，这样就证明了它所表示的所有直线必过定点（x0,y0）

2由“l1+λl2=0”求定点

在平面上如果已知两条相交直线l1：A1x+B1y+C1=0与l2：A2x+B2y+C2=0,则过l1、l2交点的直线系方程是：A1x+B1y+C1+λ(A2x+B2y+C2)=0其中λ为参数，并简写为l1+λl2=0.

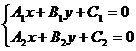根据这一道理，可知如果能把含有参数的直线方程改写成l1+λl2=0的形式，这就证明了它表示的直线必过定点，其定点的求法可由解得。

 

达标训练

（　　）A 1. 已知直线和互相平行，则它们之间的距离是：

Ａ．4 Ｂ．    Ｃ． Ｄ．

（　　）B 2. 入射光线线在直线：上，经过轴反射到直线上，再经过轴反射到直线上，则直线的方程为：

Ａ． Ｂ．      Ｃ． Ｄ．

（　　）A 3. 若直线与直线的交点在第四象限，则的取值范围是：

Ａ． Ｂ． Ｃ． Ｄ．

（　　）B 4. 直线经过一定点，则该定点的坐标为：

Ａ． Ｂ． Ｃ． Ｄ．

A 5. 设点在直线上，且到原点的距离与到直线的距离相等，则点坐标是　　　　　　．

B 6. 已知中，，，点在直线上，若的面积为，则点坐标为　　　　　　．

B 7. 直线在两坐标轴上的截距相等，且到直线的距离为，求直线的方程．

 

B 8. 一直线过点，且点到该直线距离等于，求该直线倾斜角．

 

 

 

 

 

 

A 9. 求经过两直线：和：的交点，且与直线：垂直的直线的方程．

 

 

 

 

 

B 10. 试求直线：，关于直线：对称的直线的方程．

 

 

 

 

 

 

B 11. 直线与直线，分别交于点，，若的中点是，求直线的方程．

 

 

 

 

 

B12.已知，，在轴上找一点，使，并求的值；

 

 

 

【学习反思】