福建省漳州市芗城中学高中数学 4.3空间直角坐标系教案 新人教A版必修2

一、教学目标

1、知识与技能：掌握空间直角坐标系的有关概念；会根据坐标找相应的点，会写一些简单几何体顶点的有关坐标，掌握空间两点间的距离公式，会应用距离公式解决有关问题。

2、过程与方法：通过空间直角坐标系的建立，空间两点距离公式的推导，使学生初步意识到：将空间问题转化为平面问题是解决空间问题的基本思想方法；通过本节的学习，培养学生类比，迁移，化归的能力。

3、情感态度与价值观：解析几何是用代数方法研究解决几何问题的一门数学学科，在教学过程中要让学生充分体会数形结合的思想，进行辩证唯物主义思想的教育和对立统一思想的教育；培养学生积极参与，大胆探索的精神。

二、教学重点、难点

重点：建立空间直角坐标系；

难点：用空间直角坐标系刻画点的位置和根据点的位置表示出点的坐标。

三、教学过程

（一）创设问题情景

问题1：借助平面直角坐标系，我们就可以用坐标表示平面上任意一点的位置，那么空间的点如何表示呢？

（二）知识探求

1、空间直角坐标系：

问题2：如何建立空间直角坐标系？

（1）在平面直角坐标系的基础上，通过原点再增加一根竖轴，就成了空间直角坐标系。

（2）如无特别说明，本书建立的坐标系都是右手直角坐标系。

（3）空间直角坐标系的“三要素”：原点、坐标轴方向、单位长度。

（4）在平面上画空间直角坐标系O-xyz时，一般使，，且使y轴和z轴的单位长度相同，x轴上的单位长度为y轴（或z轴）的单位长度的一半，即用斜二测的方法画。

2、思考交流：

为什么空间的点M能用有序实数对 (x，y，z) 表示？

设点M为空间直角坐标系中的一点，过点M分别作垂直于x轴、y轴、z轴的平面，依次交x轴、y轴、z轴于P、Q、R点，设点P、Q、R在x轴、y轴、z轴上的坐标分别是x、y和z，那么点M就有唯一确定的有序实数组 (x，y，z)；

反过来，给定有序实数组 (x，y，z)，可以在x轴、y轴、z轴上依次取坐标为x、y和z的点P、Q和R，分别过P、Q和R点各作一个平面，分别垂直于x轴、y轴、z轴，这三个平面的唯一的交点就是有序实数组 (x，y，z) 确定的点M。

3、例题剖析：

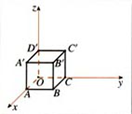
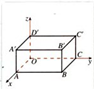
例1、如图，在长方体OABC—D1A1B1C1中，|OA| = 3，|OC| = 4，|OD1| = 2，写出D1，C，A1，B1四点的坐标。

分析：D1（0，0，2），C（0，4，0），A1（3，0，2），B1（3，4，2）。

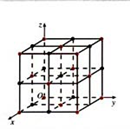
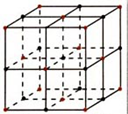
例2、结晶体的基本单位称为晶胞，如图是食盐晶胞的示意图（可看成是八个棱长为的小正方体堆积成的正方体），其中色点代表钠原子，黑点代表氯原子。如图建立空间直角坐标系Oxyz后，试写出全部钠原子所在位置的坐标。

分析：

下层钠原子的坐标：（0，0，0），（1，0，0），（1，1，0），（0，1，0）（，，0）；

中层钠原子的坐标：（，0，），（1，，），（，1，），（0，，）；

上层钠原子的坐标：（0，0，1），（1，0，1），（1，1，1），（0，1，1），（，，1）。

4、反馈练习：课本P136，练习1，2，3。

（三）知识迁移：空间两点间的距离公式

1、思考：类比平面两点间距离公式的推导，你能猜想一下空间两点间的距离公式吗？

解决问题：

（1）设点P的坐标是 (x，y，z)，求点P到坐标原点O的距离。

如图，设点P在xOy平面上的射影是B，则点B的坐标是 (x，y，0)，

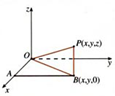在平面xOy上，有，

在Rt△OBP中，根据勾股定理，

因为 | BP | = | z |，所以。

（2）探究：如果 | OP | 是定长，那么表示什么图形？

表示空间中以原点O为圆心，r为半径的球。

（3）空间两点间的距离公式：

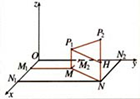
设，在平面xOy上的射影分别为，，

所以，

过点P1作P1H⊥P2N于H，则|MP1| = |z1|，|MP2| = |z2|，所以|HP2| =