| 上传:admin | 审核发布:admin | 更新时间:2015-3-29 17:41:51 | 点击次数:533次 |
河北省邯郸市馆陶县第一中学高中数学 3.1.3概率的基本性质学案 新人教A版必修3
【学习目标】1、了解事件间各种关系的概念,会判断事件间的关系;
2、了解两个互斥事件的概率加法公式、对立事件的公式,会用公式进行简单的概率计算;
3、通过学习,进一步体会概率思想方法应用于实际问题的重要性。
【重点难点】 重点:事件间的关系,概率的加法公式
难点:互斥事件与对立事件的区别与联系 ![]()
【学习内容】
一、 实践探究
在掷骰子试验中,有如下事件:
![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
还能写出如下事件:
![]() =______________________
=______________________
![]() =________________________
=________________________
![]() =________________________
=________________________
![]() =_________________________
=_________________________
![]() =_________________________
=_________________________
![]() =________________________
=________________________
![]() =_______________________
=_______________________
![]() =_____________
=_____________
二、 理论升华
1、 事件的关系与运算
(1) 包含关系:
事件C1与事件H之间的关系__________________
事件B包含事件A的定义____________________
____________________________记作__________
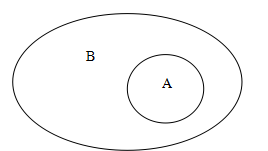 图示
图示
注:不可能事件记作![]() ,任何事件都包括不可能事件
,任何事件都包括不可能事件
(2) 相等关系
事件C1与事件D之间的关系__________________
事件B等于事件A的定义____________________
____________________________![]() __记作__________
__记作__________
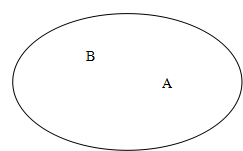 图示
图示
(3) 并事件(和事件)
事件C1、事件C6与事件K之间的关系_________
事件A与事件B的并事件的定义______________
![]() ______________________________记作__________
______________________________记作__________
 图示
图示
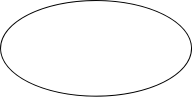
![]()
![]()
(4) 交事件(积事件)
事件D2、事件D3与事件C4之间的关系_________
事件A与事件B![]() 的交事件的定义______
的交事件的定义______![]() _____
_____![]() ___
___
______________________________记作__________
 图示
图示
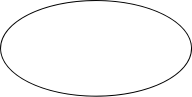
![]()
![]()
(5) 互斥事件
事件C1、C2与事件C3之间的关系_________
事件A与事件B互斥的定义______________
______________________________记作__________
图示
![]()
![]()
(6) 对立事件
事件G与事件H之间的关系_________
事件A与事件B对立的定义______________
______________________________记作__________
 图示
图示
注:互斥事件与对立事件的区别:
_____________________________________________![]() _____________________________________________________
_____________________________________________________
例1 一个射手进行一次射击,试判断下列事件哪些是互斥事件?哪些是对立事件?
事件A:命中环数大于7环 事件B:命中环数为10环;
事件C:命中环数小于6环;
事件D:命中环数为6、7、 8 、9、10环.
练习:判断下列事件是不是互斥事件?是不是对立事件?
① 某射手射击一次,命中的环数大于8与命中的环数小于8;
② 统计一个班级数学期末考试成绩,平均分不低于75分与平均分不高于75分;
③ 从装有3个红球和3个白球的口袋内任取2个球,至少有一个白球和都是红球。
2、 概率的几个基本性质
(1) 概率P(A)的取值范围________________
______________的概率为1
______________的概率为0
随机事件的概率____________
(2) 概率的加法公式:
若事件A与事件B互斥,则![]() _________
_________
(3) 对立事件的概率公式:
若事件A与事件B为对立事件,![]() 则
则![]() _______
_______
例2、某射手射击一次射中10环、9环、8环、7环的概率分别是0.24、0.28、0.19、0.16计算这名射手射击一次
(1)射中10环或9环的概率 (2)至少射中7环的概率
练习:甲乙二人下棋,和棋的概率为1/2,乙胜得概率为1/3
求(1)甲胜得概率 (2)甲不输的的概率
【课堂小结与反思】
【课后作业与练习】
1、如果某人在某比赛(这种比赛不会出现“和”的情况)中获胜的概率是0.3,那么他输的概率是多少?
2、利用简单随机抽样的方法抽查了某校200名学生。其中戴眼镜的学生有123人。如在这个学校随机调查一名学生,问他的戴眼镜的概率近似多少?
3、某工厂为了节约用电,规定每天的用电量指标为1000千瓦时,按照上个月的用电记录,30天中有12天的用电量超过指标,若第二个月仍没有具体的节电设施,试求该月第一天用电量超过指标的概率近似值
4、一个人打靶时连![]() 续射击两次,事件“至少有一次中靶”的互斥事件是( )
续射击两次,事件“至少有一次中靶”的互斥事件是( )
(A)至少有一次中靶。(B)两次都中靶。
(C)只有一次中靶。 (D![]() )两次都不中靶。
)两次都不中靶。
5、把红、蓝、黑、白4张纸牌随机分![]() 给甲、乙、丙、丁4个人,每人分得一张,事件“甲分得红牌”与事件“乙分得红牌”是( )
给甲、乙、丙、丁4个人,每人分得一张,事件“甲分得红牌”与事件“乙分得红牌”是( )
(A)对立事件 。 (B)互斥但不对立事件。
(C)不可能事件 。( D)以上都不是。
6、由![]() 经验得知,在某建设银行营业窗口排队等候存取款的人数及其概率如下:
经验得知,在某建设银行营业窗口排队等候存取款的人数及其概率如下:
|
排队人数 |
0 ~ 10 人 |
11 ~ 20 人 |
21 ~ 30 人 |
31 ~ 40 人 |
41人以上 |
|
概率 |
0.12 |
0.27 |
0.30 |
0.23 |
0.08 |
计算:(1)至多20人排队的![]() 概率;
概率;![]() (2)至少11人排队的概率。
(2)至少11人排队的概率。
通讯地址: 广州市天河区东圃黄村龙怡苑 (510660)邮箱:lzm6308@163.com 联系QQ:534386438
Copyright © 2008-2012 klxkc.com All Rights Reserved. 粤ICP备15026984号-1

