| 上传:admin | 审核发布:admin | 更新时间:2015-3-30 9:30:53 | 点击次数:815次 |
1.2 应用举例(二)
自主学习
![]() 知识梳理
知识梳理
1.在△ABC中,有以下常用结论:
(1)a+b>c,b+c>a,c+a>b;
(2)a>b⇔____________⇔____________;
(3)A+B+C=π,2=2-2;
(4)sin(A+B)=________,cos(A+B)=________,
sin 2=____________,cos 2=____________.
2.在锐角△ABC中,A+B>2⇔A>2-B⇔sin A____cos B⇔cos A____sin B.
3.三角形常用面积公式
(1)S=____________(ha表示a边上的高);
(2)S=2absin C=____________=____________;
(3)S=4R(可由正弦定理推得);
(4)S=2R2sin A·sin B·sin C(R是三角形外接圆半径);
(5)S=2r(a+b+c)(r为三角形内切圆半径).
![]() 自主探究
自主探究
在平面几何中,平行四边形的四边长的平方和等于两条对角线长的平方和.你能利用余弦定理加以证明吗?
对点讲练
知识点一 证明平面几何有关定理
![]() 例1
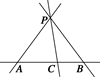
例1![]() 一条直线上有三点A,B,C,点C在点A与B之间,P是此直线外一点,设∠APC=α,∠BPC=β.求证:PC=PB+PA.
一条直线上有三点A,B,C,点C在点A与B之间,P是此直线外一点,设∠APC=α,∠BPC=β.求证:PC=PB+PA.
总结 面积法是证明平面几何问题的常用方法之一.面积等式S△ABP=S△APC+S△BPC是证明本题的关键.
变式训练1 在△ABC中,AC边上的角平分线BD交AC边于点D.求证:BC=DC.
知识点二 计算平面图形中线段的长度
![]() 例2
例2![]() 如图所示,
如图所示,
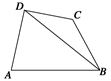
已知在四边形ABCD中,AD⊥CD,AD=10,AB=14,∠BDA=60°,∠BCD=135°,求BC的长.
总结 在解三角形时,有些复杂的问题常常需要将正弦定理、余弦定理交替使用,尽管有时不是直接求出结果,但为了过渡,也是很有必要的,本例先求BD就起到了这样的作用.
变式训练2 已知△ABC,角A、B、C所对的边长分别为a,b,c,求证:△ABC中,a边上的中线MA=2.
知识点三 计算平面图形的面积
![]() 例3
例3![]()
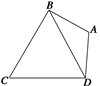
如图所示,在平面四边形ABCD中,AB=AD=1,∠BAD=θ,而△BCD是正三角形.
(1)将四边形ABCD的面积S表示为θ的函数;
(2)求S的最大值及此时θ角的值.
总结 本题将四边形面积转化为三角形面积问题,将实际问题转化为数学问题,是转化与化归思想的应用.
变式训练3 已知圆内接四边形ABCD的边长AB=2,BC=6,CD=DA=4,求圆内接四边形ABCD的面积.
![]()
1.掌握正弦定理、余弦定理及其变形形式,利用三角公式解有关三角形中的三角函数问题.
2.利用正弦定理、余弦定理解决几何问题时,关键在于找出图形中的边角的关系式,即将有关几何关系转化为三角形中的边角关系,再利用正弦定理、余弦定理求出有关量.
课时作业
一、选择题
1.△ABC的两边长分别为2,3,其夹角的余弦值为3,则其外接圆的直径为( )
A.2 B.4 C.8 D.9
2.在△ABC中,AB=7,AC=6,M是BC的中点,AM=4,则BC等于( )
A. B. C. D.
3.在△ABC中,a、b、c分别为角A、B、C的对边,如果2b=a+c,∠B=30°,△ABC的面积为2,那么b等于( )
A.2 B.1+ C.2 D.2+
4.平行四边形中,AC=,BD=,周长为18,则平行四边形的面积是( )
A.16 B.172 C.18 D.18.53
5.在△ABC中,已知b2-bc-2c2=0,a=,cos A=8,则△ABC的面积S为( )
A.2 B.
C.5 D.6
|
题 号 |
1 |
2 |
3 |
4 |
5 |
|
答 案 |
|
|
|
|
|
二、填空题
6.△ABC中,已知∠A=60°,AB∶AC=8∶5,面积为10,则其周长为________.
7.钝角三角形的三边为a,a+1,a+2,其最大角不超过120°,则a的取值范围是________.
8.已知等腰三角形的底边长为6,一腰长为12,则它的内切圆面积为________.
三、解答题
9.
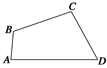
已知四边形ABCD中,AB=2,BC=CD=4,DA=6,且∠D=60°,试求四边形ABCD的面积.
10.设△ABC的内角A、B、C所对的边长分别为a、b、c,且acos B=3,bsin A=4.
(1)求边长a;
(2)若△ABC的面积S=10,求△ABC的周长l.
§1.2 应用举例(二)
知识梳理
1.(2)A>B sin A>sin B (4)sin C -cos C
cos 2 sin 2
2.> <
3.(1)2aha (2)2acsin B 2bcsin A
自主探究
证明 在△BAD内:
BD2=AB2+AD2-2AB·ADcos ∠BAD
在△ABC内:AC2=AB2+BC2-2AB·BCcos∠ABC
∵∠ABC+∠BAD=180°,
∴cos∠ABC+cos∠BAD=0.
∴BD2+AC2=2AB2+AD2+BC2,
即:AC2+BD2=AB2+BC2+CD2+DA2.
对点讲练
![]() 例1
例1![]() 证明 ∵S△ABP=S△APC+S△BPC
证明 ∵S△ABP=S△APC+S△BPC
∴2PA·PBsin(α+β)
=2PA·PCsin α+2PB·PCsin β
两边同除以2PA·PB·PC,得PC=PB+PA.
∴PC=PB+PA.
变式训练1 证明 如图所示,在△ABD中,利用正弦定理,AD=sin∠ABD.①
在△CBD中,利用正弦定理,
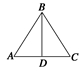
CD=sin∠DBC.②
∵BD是角B的平分线,∴∠ABD=∠CBD,
又∵∠ADB+∠CDB=180°,
∴sin∠ADB=sin∠CDB,
所以①-②,得AD=CD.即BC=DC成立.
![]() 例2
例2![]() 解 设BD=x,在△ABD中,
解 设BD=x,在△ABD中,
由余弦定理有
AB2=BD2+AD2-2AD·BD·cos∠ADB,
即142=x2+102-20xcos 60°,
∴x2-10x-96=0,
∴x=16(x=-6舍去),即BD=16.
在△BCD中,
由正弦定理sin∠CDB=sin∠BCD,
∴BC=sin 135°=8.
变式训练2 证明 如图所示:
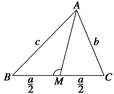
BM=MC=2.
在△ABM中,由余弦定理得:
c2=MA2+22-2MA2·cos∠AMB.
在△ACM中,由余弦定理得:
b2=MA2+22-2MA2cos∠AMC
∵cos∠AMB+cos∠AMC=0,
以上两式相加,得:b2+c2=2MA2+2.
即MA2=2b2+2c2-4a2,
∴MA=2.
![]() 例3
例3![]() 解 (1)△ABD的面积
解 (1)△ABD的面积
S1=2×1×1×sin θ=2sin θ,
由于△BDC是正三角形,所以△BDC的面积S2=4BD2.
而在△ABD中,由余弦定理可知:
BD2=12+12-2×1×1×cos θ=2-2cos θ.
于是四边形ABCD的面积S=2sin θ+4(2-2cos θ),
∴S=2+sin3,0<θ<π.
(2)由S=2+sin3及0<θ<π,
得-3<θ-3<3.
当θ-3=2时,即θ=6时,S取得最大值1+2.
变式训练3 解
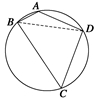
连接BD,则四边形面积
S=S△ABD+S△CBD=2AB·ADsin A+2BC·CDsin C.
∵A+C=180°,∴sin A=sin C.
∴S=2(AB·AD+BC·CD)·sin A=16sin A.
由余弦定理:在ABD中,
BD2=22+42-2·2·4cos A=20-16cos A,
在△CDB中,BD2=52-48cos C,
∴20-16cos A=52-48cos C.
又cos C=-cos A,
∴cos A=-2.∴A=120°.∴S=16sin A=8.
课时作业
1.B 2.B 3.B 4.A 5.A
6.20
解析 设AB=8k,AC=5k,k>0,
则S=2AB·AC·sin A=10k2=10.
∴k=1,AB=8,AC=5,
由余弦定理:BC2=AB2+AC2-2AB·AC·cos A
=82+52-2×8×5×2=49.
∴BC=7,
∴周长为AB+BC+CA=20.
7.2≤a<3
解析 由2,解得2≤a<3.
8.5
解析 不妨设a=6,b=c=12,由余弦定理得:
cos A=2bc=2×12×12=8,
∴sin A= 2=8.
由2(a+b+c)·r=2bcsin A
得r=5.
∴S内切圆=πr2=5π.
9.解 连结AC,在△ACD中,
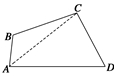
由AD=6,CD=4,∠D=60°,
可得AC2=AD2+DC2-2AD·DCcos∠D
=62+42-2×4×6cos 60°=28,
在△ABC中,由AB=2,BC=4,AC2=28,
可得cos∠B=2AB·BC
=2×2×4=-2.
又0°
所以四边形ABCD的面积
S=S△ACD+S△ABC
=2AD·CDsin∠D+2AB·BCsin∠B
=2×4×6sin 60°+2×2×4sin 120°=8.
10.
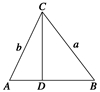
解 (1)如图,在△ABC中,作CD⊥AB,垂足为D.
∵acos B=3>0,
∴0
D在线段AB上.
由acos B=3,bsin A=4,得BD=3,CD=4.
在Rt△ABC中,a==5.
(2)由△ABC的面积S=10,得2bcsin A=10.
∵bsin A=4,∴c=5.于是,AD=2.
在Rt△ACD中,
b==2.
∴△ABC的周长l=5+5+2=10+2.
通讯地址: 广州市天河区东圃黄村龙怡苑 (510660)邮箱:lzm6308@163.com 联系QQ:534386438
Copyright © 2008-2012 klxkc.com All Rights Reserved. 粤ICP备15026984号-1

