tify: inter-ideograph;'> 

 

 

 

 

 

 

 

 

 

七、学习小结

1. 对数函数的概念、图象和性质；

2. 求定义域；

3. 利用单调性比大小.

 

知识拓展

对数函数凹凸性：函数，是任意两个正实数.

当时，；

当时，.

八、学习评价

※ 自我评价 你完成本节导学案的情况为（    ）.

  A. 很好   B. 较好   C. 一般   D. 较差

 

 

 

第一次批改	第二次批改

 

 

 

 

 

 

 

 

,

§2.2.2  对数函数及其性质（1）

一、学习目标

1. 通过具体实例，直观了解对数函数模型所刻画的数量关系，初步理解对数函数的概念，体会对数函数是一类重要的函数模型；2. 探索对数函数的单调性与特殊点；

二、学习重点：对数函数的图象，性质。            难点：学会研究函数性质的方法

三、学习方法：通过比较、对照的方法，引导学生结合图象类比指数函数，探索研究对数函数的性质，培养数形结合的思想方法，学会研究函数性质的方法.

四、学习过程

1.复习：生物机体内碳14的“半衰期”为5730年，湖南长沙马王堆汉墓女尸出土时，碳14的残余量约占原始含量的76.7%，试推算马王堆古墓的年代.（列式，课本P67，例6）

 

 

 

 

2、学习探究

探究任务一：对数函数的概

问题：根据上题，用计算器可以完成下表：

碳14的含量P	0.5	0.3	0.1	0.01	0.001
生物死亡年数t	5730	104457	20000	400000	600000

讨论：t与P的关系？

（对每一个碳14的含量P的取值，通过对应关系，生物死亡年数t都有唯一的值与之对应，从而t是P的函数）

新知：一般地，当a＞0且a≠1时，函数叫做对数函数(logarithmic function)，其中x是自变量是； 函数的定义域是（0，+∞）.

反思：

对数函数定义与指数函数类似，都是形式定义，注意辨别，如：， 都不是对数函数，而只能称其为对数型函数；对数函数对底数的限制 ，且．

探究任务二：对数函数的图象和性质（教材P₇₀~ P₇₁）

问题：你能类比前面课本P54～P56讨论指数函数性质的思路，提出研究对数函数性质的内容和方法吗？

研究方法：画出函数图象，结合图象研究函数性质．

研究内容：定义域、值域、特殊点、单调性、最大（小）值、奇偶性．

试试：同一坐标系中画出下列对数函数的图象.

（1）；                                     （2） .

解：的图象                             的图象

反思：

（1）根据图象，你能归纳出对数函数的哪些性质？

	a>1	0<a<1
图 象
性 质	(1)定义域：
	(2)值域：
	(3)过定点：
	(4)单调性：

（2）图象具有怎样的分布规律？

典型例题

例1．看会课本P71例7，         例2．看会课本P72例8

 

小结：利用单调性比大小；注意格式规范.

五、动手试试

练1. 课本P75第10题，做书上。

 

六、、当堂检测

A1. 比较下列各题中两个数值的大小.

（1）；        （2）；. （4）；

 

 

 

 

A2. 比大小：

（1）log ₆7     log ₇ 6 ； （2）log ₃1.5     log ₂ 0.8.

A3（1）. 已知下列不等式，比较正数m、n的大小：

（1）m＜n ；  （2）m＞n；

A4.（2）求下列函数的定义域.

 （1）；          （2）        .

 

 

 

 

 

 

（3），         （4）y=

 

 

A5. 当a>1时，在同一坐标系中，函数与的图象是（    ）.

 

 

 

 

 

 

 

 

 

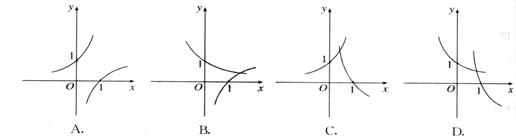
B6.已知a＞0,且a≠1,y=a^x与y=log_a(-x)函数的图象只能是下列选项中的（     ）

 

 

              

C.

                      

D                         

 

 

 

 

B7. 的定义域是           

 

B8．

 

 

 

 

 

 

 

C9.(a＞0,且a≠1)

 

 

 

C10.m＞n  (a＞1)

 

当前1/1  首页  前一页  后一页  最末页   直接到 1 页  共 0 条记录