8.2二元一次方程组的解法加减法

【学习目标】

（1）会用加减法求未知数系数相等或互为相反数的二元一次方程组的解。

（2）通过探求二元一次方程组的解法，经历用加减法把 “二元”化为“一元”的过程，体会消元的思想，以及把“未知”转化为“已知”，把复杂问题转化为简单问题的化归思想.

【学习重点】

用加减法解二元一次方程组.

【学习难点】

两个方程相减消元时，对被减的方程各项符号要做变号处理。

【自主学习】

阅读教材94—95页内容，完成下面问题：

一、问题：怎样解下面二元一次方程组呢？

二、             自学导引：

1、观察上面的方程组：

归纳：两个二元一次方程组中，同一个未知数的系数    或     时，把这两个方程的两边分别     或     ，就能消去这个未知数，得到一个         方程，这种方法就叫做加减消元法。

   ①                                                                                          

 ②

[规范解答]：

由1+2得：                                    ---第一步：加减

  将    代入①,得                                  ---第二步：求解

  所以原方程组的解为                               ---第三步：写解

【合作探究】

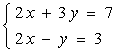  1

  2

【课堂检测】

 解下列方程：

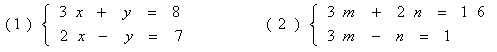
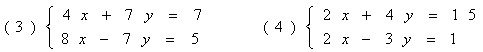
【小结】：你有何收获？还有什么疑惑的地方？