| 上传:gxda147369 | 审核发布:admin | 更新时间:2015-7-19 9:16:12 | 点击次数:704次 |
知识点一:两直线平行,同位角相等
1.如图1所示,直线a∥b,且a,b被c所截,若∠1=40°,则∠2=______.
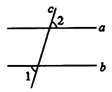
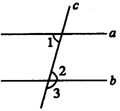
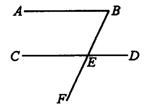
图1 图2 图3
知识点二:两直线平行,内错角相等
2.如图2所示,直线a∥b,且a,b被c所截,若∠1=60°,则∠2=_______,∠3=________.
知识点三:两直线平行,同旁内角互补
3.如图3所示,若AB∥CD,∠DEF=120°,则∠B=_______.
4.如图4所示,DE∥BC,DF∥AC,下列结论正确的个数为( )
①∠C=∠AED ②∠EDF=∠BFD ③∠A=∠BDF ④∠AED=∠DFB
A.1个 B.2个 C.3个 D.4个
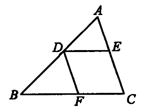
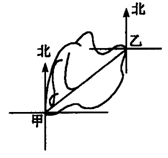
图4 图5
5.如图5,在甲,乙两地之间修一条笔直公路,从甲地测得公路的走向是北偏东50°,甲,乙两地同时开工,若干天后,公路准确接通,则乙地所修公路走向是( )
A.北偏45° B.南北方向 C.南偏西50° D.以上都不对
6.(过程探究题)如图6所示,已知CD平分∠ACB,∠EDC=![]() ∠ACB,∠DCB=30°,求∠AED度数.
∠ACB,∠DCB=30°,求∠AED度数.
[解答]因为∠1=![]() ∠ACB(已知)
∠ACB(已知)
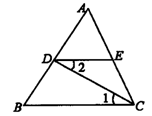 又因为∠2=
又因为∠2=![]() ∠ACB( )
∠ACB( )
所以∠1=∠2(等量代换)
即DE∥BC(内错角相等,_______)
又因为∠DCB=30°(已知) 图6
所以∠ECB=2×30°=60°
即∠AED=______=_______.
完成上述填空,理解解题过程.
答案:
1.40°
2.60°,120°
3.60°
4.D(点拨:∵DE∥BC,∴∠C=∠AED,∠EDF=∠BFD,∵DF∥AC,∴∠A=∠BDF,∵DE∥BC,DF∥AC,∴∠AED=∠DFB.)
5.C
6.已知,两直线平行,∠ECB,60°
解题规律:运用平行线性质及角平分线性质.
通讯地址: 广州市天河区东圃黄村龙怡苑 (510660)邮箱:lzm6308@163.com 联系QQ:534386438
Copyright © 2008-2012 klxkc.com All Rights Reserved. 粤ICP备15026984号-1

