| 上传:gxda147369 | 审核发布:admin | 更新时间:2015-7-22 16:00:50 | 点击次数:756次 |
3.1 勾股定理(第1课时)同步课堂训练
1.勾股定理的具体内容是: 。
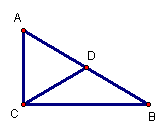 2.如图,直角△ABC的主要性质是:∠C=90°,(用几何语言表示)
2.如图,直角△ABC的主要性质是:∠C=90°,(用几何语言表示)
⑴两锐角之间的关系: ;
⑵若D为斜边中点,则斜边中线 ;
⑶若∠B=30°,则∠B的对边和斜边: ;
⑷三边之间的关系: 。
 3.△ABC的三边a、b、c,若满足b2= a2+c2,则 =90°; 若满足b2>c2+a2,则∠B是 角;
若满足b2<c2+a2,则∠B是 角。
3.△ABC的三边a、b、c,若满足b2= a2+c2,则 =90°; 若满足b2>c2+a2,则∠B是 角;
若满足b2<c2+a2,则∠B是 角。
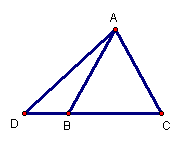
4.根据如图所示,利用面积法证明勾股定理。
5.已知在Rt△ABC中,∠B=90°,a、b、c是△ABC的三边,则
⑴c= 。(已知a、b,求c)
⑵a= 。(已知b、c,求a)
⑶b= 。(已知a、c,求b)
6.如下表,表中所给的每行的三个数a、b、c,有a<b<c,试根据表中已有数的规律,写出当a=19时,b,c的值,并把b、c用含a的代数式表示出来。
|
3、4、5 |
32+42=52 |
|
5、12、13 |
52+122=132 |
|
7、24、25 |
72+242=252 |
|
9、40、41 |
92+402=412 |
|
…… |
…… |
|
19,b、c |
192+b2=c2 |
7.在△ABC中,∠BAC=120°,AB=AC=![]() cm,一动点P从B向C以每秒2cm的速度移动,问当P点移动多少秒时,PA与腰垂直。
cm,一动点P从B向C以每秒2cm的速度移动,问当P点移动多少秒时,PA与腰垂直。
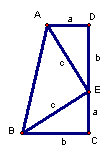
8.已知:如图,在△ABC中,AB=AC,D在CB的延长线上。
 求证:⑴AD2-AB2=BD·CD
求证:⑴AD2-AB2=BD·CD
⑵若D在CB上,结论如何,试证明你的结论。
参考答案
1.略;
2.⑴∠A+∠B=90°;⑵CD=![]() AB;⑶AC=
AB;⑶AC=![]() AB;⑷AC2+BC2=AB2。
AB;⑷AC2+BC2=AB2。
3.∠B,钝角,锐角;
4.提示:因为S梯形ABCD
= S△ABE+ S△BCE+ S△EDA,又因为S梯形ACDG=![]() (a+b)2,
(a+b)2,
S△BCE=
S△EDA=![]() ab,S△ABE=
ab,S△ABE=![]() c2,
c2, ![]() (a+b)2=2×
(a+b)2=2×![]() ab+
ab+![]() c2。
c2。
5.⑴c=![]() ;⑵a=
;⑵a=![]() ;⑶b=
;⑶b=![]()
6.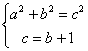 ;则b=
;则b=![]() ,c=
,c=![]() ;当a=19时,b=180,c=181。
;当a=19时,b=180,c=181。
7.5秒或10秒。
8.提示:过A作AE⊥BC于E。
通讯地址: 广州市天河区东圃黄村龙怡苑 (510660)邮箱:lzm6308@163.com 联系QQ:534386438
Copyright © 2008-2012 klxkc.com All Rights Reserved. 粤ICP备15026984号-1

