第三章 勾股定理 单元综合检测（新人教版八年级下）          (时间：45分钟，满分：100分)

一、选择题(每小题3分，共24分)

1．下列各组线段中，能够组成直角三角形的是(　　)．

A．6,7,8  B．5,6,7          C．4,5,6  D．3,4,5

2．在Rt△ABC中，已知∠C＝90°，a∶b＝3∶4，c＝10，则△ABC的面积为(　　)．

A．12  B．24  C．28  D．30

3．如图，在正方形网格中，每个小正方形的边长为1，则网格上的△ABC中，边长为有理数的边数为(　　)．

A．0            B．1            C．2            D．3

4．如图，有一块直角三角形纸片，两直角边AC＝6 cm，BC＝8 cm，现将直角边AC沿直线AD折叠，使它落在斜边AB上，且与AE重合，则CD等于(　　)．

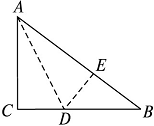
A．2 cm  B．3 cm  C．4 cm  D．5 cm

5．已知在△ABC中，AB＝8，BC＝15，AC＝17，则下列结论错误的是(　　)．

A．△ABC是直角三角形，且∠B＝90°

B．△ABC是直角三角形，且∠A＝60°

C．△ABC是直角三角形，且AC是它的斜边

D．△ABC的面积为60

6．下列命题的逆命题是真命题的是(　　)．

A．若a＝b，则|a|＝|b|                   B．全等三角形的周长相等

C．若a＝0，则ab＝0                 D．有两边相等的三角形是等腰三角形

7．三角形的三边a，b，c满足(a＋b)²－c²＝2ab，则此三角形是(　　)．

A．锐角三角形  B．直角三角形        C．钝角三角形  D．等边三角形

8．如图所示，直线l上有三个正方形a， b，c，若a，c的面积分别为5和11，则b的面积为(　　)．

A．4  B．6  C．16  D．55

二、填空题(每小题4分，共20分)

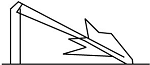
9．如图，一棵树在离地面3米处断裂，树的顶部落在离底部4米处，树折断之前有__________米高．

10．命题“直角三角形中，30°角所对的直角边等于斜边的一半”的逆命题是__________，它是__________命题．

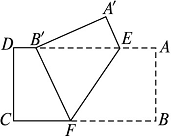
11．如图，把矩形ABCD沿EF折叠，使点B落在边AD上的点B′处，点A落在点A′处．若AE＝a，AB＝b，BF＝c，请写出a，b，c之间的一个等量关系为__________．

12．在同一地平面上有两棵树，一棵高6米，另一棵高2米，两树相距5米，一只小鸟从一棵树的树梢飞到另一棵树的树梢，则至少飞了________米．

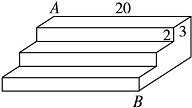
13．如图是一个三级台阶，它的每一级的长、宽和高分别为20 dm,3 dm,2 dm，A和B是这个台阶两个相对的端点，A点有一只蚂蚁，想到B点去吃可口的食物，则蚂蚁沿着台阶面爬到B点的最短路程是__________dm.

三、解答题(共56分)

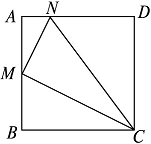
14．(本小题满分10分)如图所示，隔湖有A，B两点，从与BA方向成直角的BC方向上取一个点C，测得CA＝50 m，CB＝40 m，试求A，B两点间的距离．

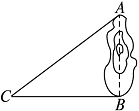
15．(本小题满分10分)为了减少交通事故的发生，“中华人民共和国道路交通管理条例”规定：小汽车在城市街道上行驶速度不得超过70 km/h.如图，一辆小汽车在一条由东向西的城市街道上直道行驶，某一时刻刚好行驶到路边车速监测仪的正前方30 m处，过了2 s后，测得小汽车与车速监测仪的距离为50 m，问这辆小汽车超速了吗？

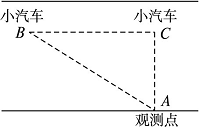
16．(本小题满分12分)如图所示，在正方形ABCD中，M为AB的中点，N为AD上的一点，且AN＝AD，试猜测△CMN是什么三角形，请证明你的结论．

17．(本小题满分12分)[问题情境]

勾股定理是一条古老的数学定理，它有很多种证明方法，我国汉代数学家赵爽根据弦图，利用面积法进行证明，著名数学家华罗庚曾提出把“数形关系”(勾股定理)带到其他星球，作为地球人与其他星球“人”进行第一次“谈话”的语言．

[定理表述]

请你根据图1中的直角三角形叙述勾股定理(用文字及符号语言叙述)．

            

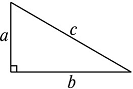
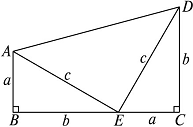
图1                                     图2

[尝试证明]

以图1中的直角三角形为基础，可以构造出以a，b为底，以a＋b为高的直角梯形(如图2)，请你利用图2，验证勾股定理．

[知识拓展]

利用图2中的直角梯形，我们可以证明.其证明步骤如下：

∵BC＝a＋b，AD＝__________，

又∵在直角梯形ABCD中有BC__________AD(填大小关系)，即__________，

∴.

18．(本小题满分12分)如图，正方形网格MNPQ中，每个小方格的边长都相等，正方形ABCD的顶点在正方形MNPQ的4条边的小方格顶点上．

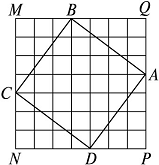
(1)设正方形MNPQ网格内的每个小方格的边长为1，求：

①△ABQ，△BCM，△CDN，△ADP的面积；

②正方形ABCD的面积．

(2)设MB＝a，BQ＝b，利用这个图形中的直角三角形和正方形的面积关系，你能验证已学过的哪一个数学公式或定理吗？

 

参考答案

1. 答案：D

2. 答案：B　设a＝3x(x＞0)，则b＝4x.根据勾股定理，得(3x)²＋(4x)²＝10².求得△ABC的两直角边的长分别为6和8，其面积为24.

17. 答案：B　由勾股定理，得AB＝，BC＝，AC＝＝5.由此可以看出，只有AC的长度是有理数．

4. 答案：B　由勾股定理得，AB＝＝10 cm，由折叠知AC＝AE＝6 cm，设CD＝DE＝x cm，则BE＝AB－AE＝4 cm，DB＝(8－x) cm.

在Rt△DEB中，DE²＋BE²＝DB²，

即x²＋4²＝(8－x)²，解得x＝17.故CD＝3 cm.

5. 答案：B　因为AB²＋BC²＝8²＋15²＝17²＝AC²，所以△ABC是直角三角形，且AC为斜边，AC所对的角∠B＝90°，△ABC的面积＝AB·BC＝60，无法推出∠A＝60°.

6. 答案：D　A的逆命题是若|a|＝|b|，则a＝b.假命题；B的逆命题是周长相等的三角形是全等三角形．假命题；C的逆命题是若ab＝0，则a＝0.假命题；D的逆命题是等腰三角形的其中两边相等．真命题．

7. 答案：B　(a＋b)²－c²＝2ab，则a²＋b²＋2ab－c²＝2ab，

即a²＋b²＝c²，此三角形是直角三角形．

8. 答案：C　由题意易得图形中的两个直角三角形是全等的．

所以由勾股定理可得S_b＝S_a＋S_c＝5＋11＝16.

9. 答案：8

10. 答案：在直角三角形中，如果一条直角边等于斜边的一半，那么这条直角边所对的角等于30°　真　把题中的结论作为条件，把条件作为结论，可知此命题为真命题．

11. 答案：c²＝a²＋b²　在Rt△A′B′E中，A′E＝AE＝a，A′B′＝AB＝b，

BF＝B′F＝B′E＝c，∴c²＝a²＋b².

12. 答案：

117. 答案：25　如图，由题意知AC＝20，BC＝15，则AB＝＝25.

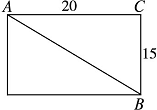
所以最短路程是25 dm.

14. 解：在Rt△ABC中，由勾股定理得AB＝＝30(m)．

答：A，B两点间的距离是30 m.

15. 解：小汽车超速了．

理由：由勾股定理，得BC＝＝40，

所以小汽车的速度是40÷2＝20(m/s)．

因为20 m/s＝72 km/h＞70 km/h，

所以小汽车超速了．

16. 解：猜想△CMN是直角三角形．

设正方形ABCD的边长为4a，

则AM＝2a，AN＝a，DN＝3a.

在Rt△AMN中

由勾股定理得，MN²＝5a².同理可得CN²＝25a²，

CM²＝20a².

所以MN²＋CM²＝CN².

所以△CMN是直角三角形．

17. 解：[定理表述]

如果直角三角形的两直角边长分别为a，b，斜边长为c，那么a²＋b²＝c².

[尝试证明]∵Rt△ABE≌Rt△ECD，∴∠AEB＝∠EDC.又∠EDC＋∠DEC＝90°，

∴∠AEB＋∠DEC＝90°.

∴∠AED＝90°.

∵S_梯形ABCD＝S_Rt△ABE＋S_Rt△DEC＋S_Rt△AED，

∴(a＋b)(a＋b)＝ab＋ab＋c².

整理，得a²＋b²＝c².

[知识拓展]

　＜　a＋b＜

18. 解：(1)①S_△ABQ＝AQ·BQ＝×3×4＝6，

S_△BCM＝BM·CM＝×3×4＝6，

S_△CDN＝CN·DN＝×3×4＝6，

S_△ADP＝DP·AP＝×3×4＝6.

②S_{正方形ABCD}＝S_{正方形MNPQ}－S_△ABQ－S_△BCM－S_△CDN－S_△ADP＝7²－6－6－6－6＝25.

(2)验证了勾股定理，证明过程如下：

设AB＝c，

S_{正方形ABCD}＝S_{正方形MNPQ}－S_△ABQ－S_△BCM－S_△CDN－S_△ADP，即c²＝ (a＋b)²－ab－ab－ab－ab，

∴c²＝a²＋b²，

即直角三角形中两直角边长的平方和等于斜边长的平方．