| 上传:gxda147369 | 审核发布:admin | 更新时间:2015-7-22 16:28:03 | 点击次数:831次 |
第17章《勾股定理》复习测试 新人教版
一、选择题(每题2分,共26分)
1、如果梯子的底端离建筑物5米,13米长的梯子可以达到该建筑![]() 物的高度是 ( )
物的高度是 ( )
A. 12米 B. 13 C. 14米 D. 15米
2、已知x、y为正数,且│x2-4│+(y2-3)2=0,如果以x、y的长为直角边作一个直角三角
形那么以这个直角三角形的斜边为边长的正方形的面积为( );
A、5 B、25 C、7 D、15
3、在△ABC中,∠C=90°,周长为60,斜边与一直角边比是13∶5,则这个三角形三边长分别是( )
A.5,4,3 B.13,12,5 C.10,8,6 D.26,24,10
4、在直角坐标系中,点P(-2,3)到原点的距离是 ( )
A 、![]() B、
B、![]() C、
C、![]() D、2
D、2
5、若将直角三角形的两直角边同时扩大2倍,则斜边扩大为原来的( );
A、2倍 B、3倍 ![]() C、4倍
D、5倍
C、4倍
D、5倍
6、下列各组线段中的三个长度①9、12、15;②7、24、25;③32、42、52;④3a、4a、5a(a>0);
⑤m2-n2、2mn、m2+n2(m、n为正整数,且m>n)其中可以构成直角三角形的有( );
A、5组; B、4组; C、3组; D、2组
7、如果正方形ABCD的面积为![]() ,则对角线AC的长度为( );
,则对角线AC的长度为( );
 A、
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
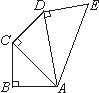
8、如图,![]() ,
,![]() 且
且![]() ,
,
![]() ,
,![]() ,则线段AE的长为( );
,则线段AE的长为( );
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
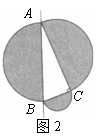
9、如图2,分别以直角△ABC的三边AB,BC,CA为直径向外作半圆.设直线AB左边阴影部分的面积为S1,右边阴影部分的面积和为S2,则![]() ( )
( )
A.S1=S2 B.S1<S2 C.S1>S2 D.无法确定
10、若△ABC的三边a、b、c满足a2+b2+c2+338=10a+24b+26c,则此三角形为( );
A、锐角三角形 B、钝角三角形 C、直角三角形 D、不能确定
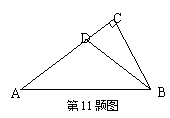
11、如图,在Rt△ABC中,∠C=90°,D为AC上一点,且DA=DB=5,又△DAB的面积为10,
那么DC的长是( );
 A、4 B、3 C、5 D
A、4 B、3 C、5 D![]() 、4.5
、4.5
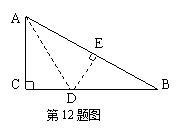
12、如图,一块直角三角形的纸片,两直角边![]() AC
AC![]() =6㎝,BC=8㎝,现将直角边AC沿直线AD折
=6㎝,BC=8㎝,现将直角边AC沿直线AD折
叠,使它落在斜边AB上,且与AE重合,则CD等于( );
A、2㎝ B、3㎝ C、4㎝ D、5㎝
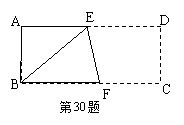
13、已知,如图长方形ABCD中,AB=3cm,AD=9cm,将此长方形折叠,使点B与点D重合,折
痕为EF,则△ABE的面积为(![]() ).
).
A、6cm2 B、8cm2 C、10cm2 D、12cm2
二、填空题(每题2分,共18分)
14、在△ABC中,点D为BC的中点,BD=3,AD=4,AB=5,则AC=_________________;
15、命题“同位角相等,两直线平行”的逆命题是_____________________________;
16、如图是2002年北京第24届国际数学家大会会徽,由4个全等的直角三角形拼合而成,
![]()
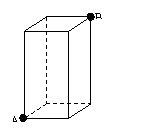
 若图中大小正方形的面积分别为52和4,则直角三角形的两直角边分别为_________
;
若图中大小正方形的面积分别为52和4,则直角三角形的两直角边分别为_________
;

(第16题)
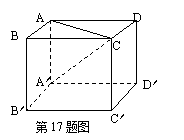
17、 如图,正方形ABCD—A′B′C′D′的棱长为3,那么AC2=_______,A′C2=________;
18、一只蚂蚁从长、宽都是3,高是8的长方体纸箱的A点沿纸箱爬到B点,那么它所行的最
短路线的长是______________________;![]()
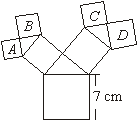
19、如图所示的图形中,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最
大的正方形的边长为7 cm,则正方形A、B、C、D的面积的和是_______________![]() ;
;
20、直角三角形两直角边长分别为5和12,则它斜边上的高为_______.
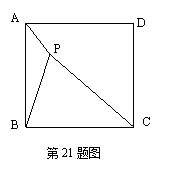
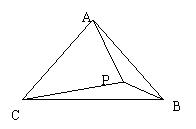 21、如图,P为正方形ABCD内一点,PA=1,PB=2,PC=3,则∠APB=_______
.
21、如图,P为正方形ABCD内一点,PA=1,PB=2,PC=3,则∠APB=_______
.
22、在△ABC中,∠ACB=90°,AC=BC,P是△ABC内一点,且PA=6,PB=2,PC=4,∠BPC=_______ .
三、解答题(共56分)
23、如图,一架长2.5 m的梯子,斜靠在一竖直的墙上,这时,梯底距墙底端0.7 m,如果梯
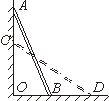 子的
子的![]() 顶端
顶端![]() 沿墙下滑0.4 m,则梯子的底端将滑出多少米?
沿墙下滑0.4 m,则梯子的底端将滑出多少米?
24、小明从家出发向正东方向走了160千米,然后又向正北出发走到离家200千米远的地方。小明向正北方向走了多远?
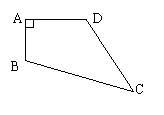
25、已知,如图,四边形ABCD中,AB=3cm,AD=4cm,BC=13cm,CD=12cm,且∠A=90°,求四
边形ABCD的面积.
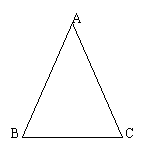
26、如图,在△ABC中,AB=AC
(1)P为BC上的中点,求证:AB2-AP2=PB·PC;
(2)若P为BC上的任意一点,(1)中的结论是否成立,并证明;
(3)若P为BC延长线上一点,说明AB、AP、PB、PC之间的数量关系.
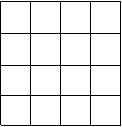
27、如图,正方形网格中的每个小正方形边长都是1,任意连结![]() 这些小正方形的顶点,可得到一些线段
这些小正方形的顶点,可得到一些线段![]() 。请在图中画出
。请在图中画出![]() 这样的线段,并选择其中的一个说明这样画的道理。
这样的线段,并选择其中的一个说明这样画的道理。
 28、如图,一个牧童在小河的南4km的A处牧马,而他正位于他的小
28、如图,一个牧童在小河的南4km的A处牧马,而他正位于他的小![]() 屋B的西8km北7km处,他想把他的马牵到小河边去饮水,然后回家.他要完成这件事情所走的最短路程是多少?
屋B的西8km北7km处,他想把他的马牵到小河边去饮水,然后回家.他要完成这件事情所走的最短路程是多少?
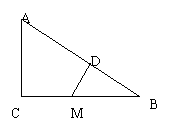 29、在△ABC中,∠C=90°,M是BC的中点,MD⊥AB于D,求证:
29、在△ABC中,∠C=90°,M是BC的中点,MD⊥AB于D,求证:![]() ;
;
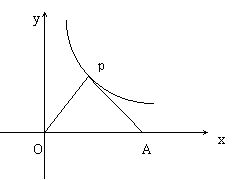 30、已知点P(m,n)(m﹥0)在反比例函数
30、已知点P(m,n)(m﹥0)在反比例函数![]() 上,连OP,作PA⊥OP,交x轴于A
上,连OP,作PA⊥OP,交x轴于A
点,A点坐标为(a,o)(a>m);![]()
(1)当n=1时,求P点坐标;(2)当PA=OP,求k的大小;
通讯地址: 广州市天河区东圃黄村龙怡苑 (510660)邮箱:lzm6308@163.com 联系QQ:534386438
Copyright © 2008-2012 klxkc.com All Rights Reserved. 粤ICP备15026984号-1

