| 上传:gxda147369 | 审核发布:admin | 更新时间:2015-8-11 11:21:31 | 点击次数:447次 |

轴对称、平移、旋转是平面几何的三大变换。由一个平面图形变为另一个平面图形,并使这两个图形关于某一条直线成轴对称,这样的图形改变叫做图形的轴对称变换。轴对称具有这样的重要性质: (1)成轴对称的两个图形全等;(2)如果两个图形成轴对称,那么对称轴是对称点连线的垂直平分线。中考压轴题中轴对称 (折叠)问题,包括有关三角形的轴对称性问题;有关四边形的轴对称性问题;有关圆的轴对称性问题;有关利用轴对称性求最值问题;有关平面解析几何中图形的轴对称性问题。
一. 有关三角形的轴对称性问题
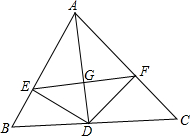
原创模拟预测题1. 如图,AD是△ABC的角平分线,DE⊥AB,DF⊥AC,垂足分别是点E,F,连接EF,交AD于点G,求证:AD⊥EF.

原创模拟预测题2. 如图,在Rt△ABC中,∠C=900,∠B=300,BC=![]() ,点D是BC边上一动点(不与点B、C重合),过点D作DE⊥BC交AB边于点E,将∠B沿直线DE翻折,点B落在射线BC上的点F处,当△AEF为等腰三角形时,BD的长为 。
,点D是BC边上一动点(不与点B、C重合),过点D作DE⊥BC交AB边于点E,将∠B沿直线DE翻折,点B落在射线BC上的点F处,当△AEF为等腰三角形时,BD的长为 。

【答案】![]() 。
。
【考点】翻折问题,轴对称的性质,锐角三角函数定义,特殊角的三角函数值,勾股定理,等腰三角形的判定,分类思想的应用。

二. 有关四边形的轴对称性问题
原创模拟预测题3. 如图①是3×3菱形格,将其中两个格子涂黑,并且使得涂黑后的整个图案是轴对称图形,约定绕菱形ABCD的中心旋转能重合的图案都视为同一种,例②中四幅图就视为同一种,则得到不同共有【 】
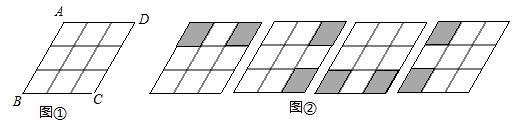
A.4种 B.5种 C.6种 D.7种
【答案】B。
【考点】利用旋转的轴对称设计图案。
【分析】根据轴对称的定义及题意要求画出所有图案后即可得出答案:
得到的不同图案有:

共5个。故选B。
原创模拟预测题4. 如图,△ABC中,已知∠BAC=45°,AD⊥BC于D,BD=2,DC=3,求AD的长。
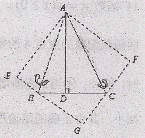
小萍同学灵活运用了轴对称知识,将图形进行翻折变换,巧妙地解答了此题。
(1)分别以AB、AC为对称轴,画出△ABD、△ACD的轴对称图形,D、C点的对称点分别为E、F,延长EB、FC相交于G点,求证:四边形AEGF是正方形;
(2)设AD=x,利用勾股定理,建立关于x的方程模型,求出x的值。
【答案】(1)由翻折变换可得∠E=∠ADB=90°,EB=BD=2,CF=CD=3,∠F=∠ADC=90°,AE=AD,AF=AD,再结合可得四边形AEGF为矩形,再有AE=AF=AD,即可证得结论;(2)6
【解析】
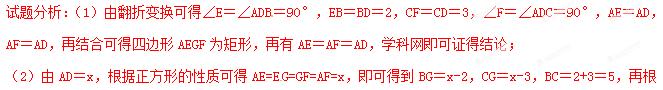
据勾股定理即可列方程求得结果.
在Rt△BGC中,![]()
解得![]() (不合题意,舍去)
(不合题意,舍去)
∴AD=x=6.

考点:翻折变换,正方形的判定,勾股定理
点评:解答本题的关键是熟练掌握翻折变换的性质:翻折前后图形的对应边或对应角相等;有四个角是直角的四边形是矩形,有一组邻边相等的矩形是正方形.
原创模拟预测题5. 菱形ABCD中,∠ABC=450,点P是对角线BD上的任一点,点P关于直线AB、AD、CD、BC的对称点分别是点E、F、G、H, BE与DF相交于点M,DG与BH相交于点N,证明:四边形BMDN是正方形。
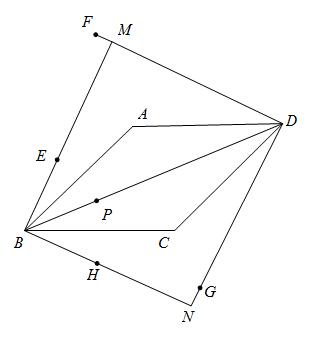
【答案】∵四边形ABCD是菱形,
∴∠ABD=∠DBC=∠ADB=∠BDC。
∵∠ABC=450,点P关于直线AB、AD、CD、BC的对称点分别是点E、F、G、H,
∴∠MBN=∠MDN=900,∠MBC=∠MDB=450。
∴△BDM是等腰直角三角形。
∴∠BMD=900,BM=DM。
∴四边形BMDN是正方形。
【考点】菱形的性质,轴对称的性质,正方形的判定,等腰直角三角形的判定和性质。

三. 有关圆的轴对称性问题
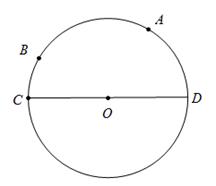
原创模拟预测题6. 如图,已知⊙O的直径CD为4,弧AC的度数为120°,弧BC的度数为30°,在直径CD上作出点P,使BP+AP的值最小,若BP+AP的值最小,则BP+AP的最小值为 。
【答案】![]() 。
。
【考点】圆的综合题,轴对称(最短路线问题),弧、圆心角和圆周角的关系,等边三角形的性质,锐角三角函数定义,特殊角的三角函数值,相似三角形的判定和性质,配方法的应用。
【分析】如图,过B点作弦BE⊥CD,连接AE交CD于P点,连接PB,则点P 即为使BP+AP的值最小的点。
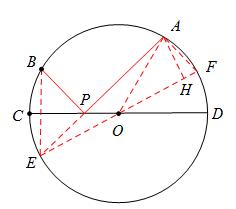

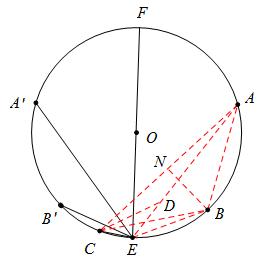
原创模拟预测题7. 已知A,B,C为⊙O上相邻的三个六等分点,点E在劣弧AC上(不与A,B,C重合),EF
为⊙O的直径,将⊙O沿EF折叠,使点A与A′重合,点B与B′重合,连接EB′,EC,EA′。设EB′=b,EC=c,EA′=p。试探究b,c,p三者的数量关系。
【答案】如图1,若点E在弧AB上,连接AB、AC、BC,
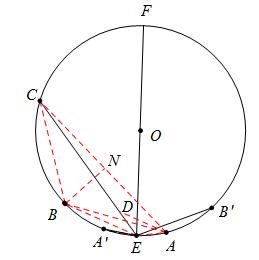
由题意,点A、B、C为圆上的六等分点,
∴AB=BC,![]() 。
。
在等腰△ABC中,过顶点B作BN⊥AC于点N,
则AC=2CN=2BC•cos∠ACB=2cos300•BC,
∴![]() 。
。
连接AE、BE,在CE上取一点D,使ED=EA,连接AD,

∴c = p +![]() 。
。

∵∠ABC=∠CED,
∴△ABC与△CED为顶角相等的两个等腰三角形。
∴△ABC∽△CED。∴![]() ,∠ACB=∠DCE。
,∠ACB=∠DCE。
∵∠ACB=∠ACD+∠BCD,∠DCE=∠BCE+∠BCD,∴∠ACD=∠BCE。
在△ACD与△BCE中,∵![]() ,∠ACD=∠BCE,∴△ACD∽△BCE。
,∠ACD=∠BCE,∴△ACD∽△BCE。
∴![]() 。∴
。∴![]() 。
。
∴EA=ED+DA=EC+![]() 。
。
由折叠性质可知,p=EA′=EA,b=EB′=EB,c=EC。
∴p=c+![]() 。
。
【考点】圆的综合题,折叠问题,圆周角定理,等腰三角形的性质,相似三角形的判定和性质,锐角三角函数定义,分类思想的应用。
【分析】分点E在弧AB上和点E在弧BC上两种情况讨论,分别根据折叠的性质,综合应用圆周角定理,等腰三角形的性质,相似三角形的判定和性质,锐角三角函数定义求解即可。
四. 有关利用轴对称性求最值问题
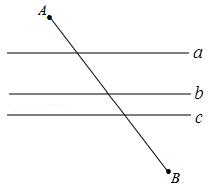
原创模拟预测题8. 如图,已知直线a∥b∥c,且a与b之间的距离为3,且b与c之间的距离为1,点A到直线a的距离为2,点B到直线c的距离为3,AB=![]() .试在直线a上找一点M,在直线c上找一点N,满足MN⊥a且AM+MN+NB的长度和最短,则此时AM+NB=【 】
.试在直线a上找一点M,在直线c上找一点N,满足MN⊥a且AM+MN+NB的长度和最短,则此时AM+NB=【 】
A.12 B.10 C.8 D.6
【答案】C。
【考点】轴对称的应用(最短线路问题),平行线之间的距离,平行四边形的判定和性质,勾股定理。
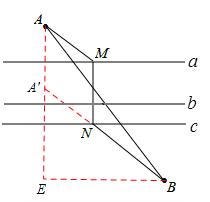
【分析】MN表示直线a与直线c之间的距离,是定值,只要满足AM+NB的值最小即可,如图,作点A关于直线a的对称点A′,连接A′B交直线c与点N,过点N作NM⊥直线a,连接AM,


原创模拟预测题9. 已知抛物线![]() :
:![]() 的顶点在坐标轴上.
的顶点在坐标轴上.
(1)求![]() 的值;
的值;
(2)![]() 时,抛物线
时,抛物线![]() 向下平移
向下平移![]() 个单位后与抛物线
个单位后与抛物线![]() :
:![]() 关于
关于![]() 轴对称,且
轴对称,且![]() 过点
过点![]() ,求
,求![]() 的函数关系式;
的函数关系式;
(3)![]() 时,抛物线
时,抛物线![]() 的顶点为
的顶点为![]() ,且过点
,且过点![]() .问在直线
.问在直线![]() 上是否存在一点
上是否存在一点![]() 使得△
使得△![]() 的周长最小,如果存在,求出点
的周长最小,如果存在,求出点![]() 的坐标,
如果不存在,请说明理由.
的坐标,
如果不存在,请说明理由.
【答案】.解:当抛物线![]() 的顶点在
的顶点在![]() 轴上时
轴上时
![]()
解得![]() 或
或![]() ………………………………1分
………………………………1分
当抛物线![]() 的顶点在
的顶点在![]() 轴上时
轴上时
![]()
∴![]() ………………………………2分
………………………………2分
综上![]() 或
或![]() .
.

∴![]() ,
,![]() ,
,![]() …………………………………3分
…………………………………3分
∴抛物线![]() :
: ![]()
∵![]() 过点
过点![]()
∴![]() ,即
,即![]() ……………………………………4分
……………………………………4分
解得![]() (由题意
(由题意![]() ,舍去)∴
,舍去)∴![]()
∴抛物线![]() :
: ![]() . ………………………………………………5分
. ………………………………………………5分

【解析】略
五. 有关平面解析几何中图形的轴对称性问题
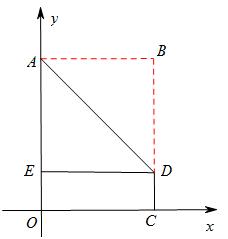
原创模拟预测题10. 将矩形OABC置于平面直角坐标系中,点A的坐标为(0,4),点C的坐标为(m,0)(m>0),点D(m,1)在BC上,将矩形OABC沿AD折叠压平,使点B落在坐标平面内,设点B的对应点为点E,当△ADE是等腰直角三角形时,m= ,点E的坐标为 ;

【答案】3;(0,1)。
【考点】折叠问题,矩形的性质,折叠的对称性质,正方形的判定和性质。

原创模拟预测题11. 如图,已知抛物线y=ax2+bx+c(a≠0)的顶点坐标为(4,![]() ),且与y轴交于点C(0,
),且与y轴交于点C(0,![]() ),与x轴交于A,B两点(点A在点B的左边)。
),与x轴交于A,B两点(点A在点B的左边)。
(1)求抛物线的解析式及A,B两点的坐标;
(2)在(1)中抛物线的对称轴l上是否存在一点P,使AP+CP的值最小?若存在,求AP+CP的最小值,若不存在,请说明理由。
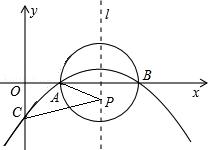

(2)存在。
如图,由(1)知:抛物线的对称轴l为x=4,
因为A、B两点关于l对称,连接CB交l于点P,则AP=BP,所以AP+CP=BC的值最小。
∵B(6,0),C(0,2),∴OB=6,OC=2。∴BC=2![]() 。
。
∴AP+CP=BC=2![]() 。
。
∴AP+CP的最小值为2![]() 。
。
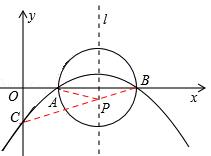
【考点】二次函数综合题,待定系数法的应用,曲线上点的坐标与方程的关系,二次函数的性质,轴对称的应用(最矩线路问题),勾股定理。

通讯地址: 广州市天河区东圃黄村龙怡苑 (510660)邮箱:lzm6308@163.com 联系QQ:534386438
Copyright © 2008-2012 klxkc.com All Rights Reserved. 粤ICP备15026984号-1

