| 上传:admin | 审核发布:admin | 更新时间:2015-3-30 11:11:24 | 点击次数:793次 |
河北省石家庄市第一中学高中数学 3.1不等关系与不等式(2)教案 新人教A版必修5
教学目标:
1.知识与技能:
掌握不等式的基本性质,会用不等式的性质证明简单不等式,掌握比较大小的方法.
2.过程与方法:
通过解决具体问题,学会依据具体问题的实际背景分析问题、解决问题的方法.
3.情感、态度与价值观:
通过解决具体问题,体会数学在生活中的重要作用,培养严谨的思维习惯.
重 点:不等式的概念和比较大小的方法.
难 点:比较大小的方法.
教学过程:
一、 不等式的概念
1.同向不等式、异向不等式的概念:
同向不等式:如:![]() 与
与![]() ;
;![]() 与
与![]() .
.
异向不等式:如:![]() 与
与![]() .
.
2.数运算性质与大小顺序之间的关系:
![]() ;
;
![]() ;
;
![]() .
.
二、判断实数大小的方法:
1.差比法:
例1.比较![]() 与
与![]() 的大小;
的大小;
解:![]()
![]()
![]() .
.
其中等号当且仅当![]() ,即
,即![]()
![]() 时成立.
时成立.
例2.设![]() ,比较
,比较![]() 与
与![]() 的大小.
的大小.
方法1:![]()
![]()
![]() .
.
方法2:(主元法)
![]()
![]() .(也可以证明判别式不大于零).
.(也可以证明判别式不大于零).
例3.已知![]() 是实数,试比较
是实数,试比较![]() 与
与![]() 的大小.
的大小.
解:∵ ![]()
![]()
![]()
∴ 当![]() 时,
时,![]()
![]() ;
;
当![]() 且
且![]() 时,
时,![]()
![]() ;
;
当![]() 时,
时,![]()
![]() .
.
练习:比较![]() 与
与![]() 的大小.
的大小.
解:![]()
![]() .
.
其中等号当且仅当![]() 时成立.即
时成立.即![]()
![]() .
.
小结:①作差;②变形;③判断差的符号(与两个实数本身的符号无关).
2.商比法:
例4.设![]() ,试比较
,试比较![]() 与
与![]() 的大小.
的大小.
解:![]() 又
又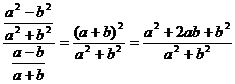 .
.
![]() ,∴ 上式大于1,
,∴ 上式大于1,
∴ ![]() >
>![]() .
.
小结:对任意两个正实数![]() 、
、![]() ,若
,若![]() ,则
,则![]() ;若
;若![]() ,则
,则![]() ;若
;若![]() ,则
,则![]() ;反之亦成立.
;反之亦成立.
练习:若![]() ,比较
,比较![]() 与
与![]() 的大小.
的大小.
解法一:![]()
![]() =
=![]()
∵ ![]() ,∴
,∴ ![]() ,
,![]() .
.
∴ ![]()
![]() .
.
解法二:![]() .
.
![]()
![]() ,
,![]() .
.
根据函数![]() 在R上是增函数,则
在R上是增函数,则![]() .
.
![]()
![]() 且
且![]() ,则
,则![]() <
<![]() .
.
例5.设![]() ,
,![]() 且
且![]() ,比较
,比较![]() 与
与![]() 的大小.
的大小.
解法一:![]() .
.
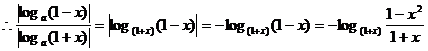
![]() .
.
![]() .
.
解法二:![]()
![]()
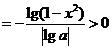
![]() .
.
说明:(1)用求差比较结果时,通常是做因式分解,利用各因式的符号判断,或是配方利用非负数的性质进行判断.
(2)用求商比较结果时应注意与1的大小时,通常不等式两边是以积商幂的形式出现,求商时应注意分母必须大于零,且注意研究比值特征,利用函数性质来判断.
三、作业:

通讯地址: 广州市天河区东圃黄村龙怡苑 (510660)邮箱:lzm6308@163.com 联系QQ:534386438
Copyright © 2008-2012 klxkc.com All Rights Reserved. 粤ICP备15026984号-1

