1.3　函数的基本性质

1．3.1　单调性与最大(小)值

 

1．若函数y＝(2k＋1)x＋b在R上是减函数，则…

(　　)

　　　 　　　　　 　　　　　

 

A．k＞                    B．k＜

C．k＞－                  D．k＜－

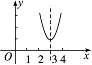
2．函数y＝x²－6x＋10在区间(2,4)上是…(　　)

A．递减函数                B．递增函数

C．先递减再递增            D．先递增再递减

3．如果函数f(x)在[a，b]上是增函数，对于任意的x₁、x₂∈[a，b](x₁≠x₂)，则下列结论中不正确的是

(　　)

A.>0

B．(x₁－x₂)[f(x₁)－f(x₂)]＞0

C．f(a)＜f(x₁)＜f(x₂)＜f(b)

D.>0

4．下图表示某市2008年6月份某一天的气温随时间变化的情况，请观察此图回答下列问题：

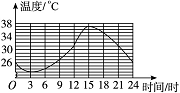
(1)这天的最高气温是__________；

(2)这天共有______个小时的气温在31 ℃以上；

(3)这天在______(时间)范围内温度在上升；

(4)请你预测一下，次日凌晨1点的气温大约在______内．

 

课堂巩固

 

1．已知函数f(x)在(－∞，＋∞)上是增函数，a，b∈R，且a＋b>0，则有(　　)

A．f(a)＋f(b)>－f(a)－f(b)

B．f(a)＋f(b)<－f(a)－f(b)

C．f(a)＋f(b)>f(－a)＋f(－b)

D．f(a)＋f(b)<f(－a)＋f(－b)

2．若函数f(x)＝x²＋2(a－1)x＋2在区间(－∞，4)上是减函数，则实数a的取值范围是… (　　)

A．a≤－3                 B．a≥－3

C．a≤5                   D．a≥3

3．函数y＝x＋(　　)

A．有最小值，无最大值

B．有最大值，无最小值

C．有最小值，最大值2

D．无最大值，也无最小值

4．函数y＝的单调递减区间为(　　)

A．(－∞，－3]             B．(－∞，－1]

C．[1，＋∞)               D．[－3，－1]

5．若y＝ax，y＝－在(0，＋∞)上都是减函数，则y＝ax²＋bx在(0，＋∞)上是__________函数．(选填“增”或“减”)

6．一次函数f(x)是减函数，且满足f[f(x)]＝4x－1，则f(x)＝__________.

7．证明函数f(x)＝x＋在(0,1)上是减函数．

 

 

 

 

 

 

 

 

 

 

 

 

8．已知函数f(x)＝3x＋2，x∈[－1,2]，证明该函数的单调性并求出其最大值和最小值．

 

 

 

 

 

 

 

 

1．设函数f(x)是(－∞，＋∞)上的减函数，则(　　)

A．f(a)>f(2a)                  B．f(a²)<f(a)

C．f(a²＋a)<f(a)                D．f(a²＋1)<f(a)

2．已知0<t≤，那么－t的最小值是… (　　)

A.  B.  C．2  D．－2

3．若函数y＝mx²＋x＋5在[－2，＋∞)上是增函数，则m的取值范围是(　　)

A．{m|0≤m≤}                B．{m|0<m≤}

C．{m|0≤m<}                  D．{m|0<m<}

4．函数f(x)＝x²－4x＋5在区间[0，m]上的最大值为5，最小值为1，则m的取值范围是(　　)

A．[2，＋∞)                     B．[2,4]

C．(－∞，2]                     D．[0,2]

5．已知函数f(x)＝3－2|x|，g(x)＝x²－2x，构造函数F(x)，定义如下：当f(x)≥g(x)时，F(x)＝g(x)；当f(x)<g(x)时，F(x)＝f(x)，那么F(x)(　　)

A．有最大值3，最小值－1

B．有最大值3，无最小值

C．有最大值7－2，无最小值

D．无最大值，也无最小值

6．(2009广西北海一检，文10)已知函数f(x)＝是(－∞，＋∞)上的减函数，那么a的取值范围是(　　)

A．(0,3)                          B．(0,3]

C．(0,2)                          D．(0,2]

7．将长度为1的铁丝分成两段，分别围成一个正方形和一个圆形．要使正方形和圆的面积之和最小，则正方形的周长应为__________．

8．已知y＝f(x)在定义域(－1,1)上是减函数，且f(1－a)＜f(3a－1)，则a的取值范围是__________．

9．已知函数f(x)＝kx²－4x－8在[5,20]上是单调函数，求实数k的取值范围．

 

 

 

 

 

 

 

 

 

 

10．已知函数f(x)＝，x∈[1,3]，求函数的最大值和最小值．

 

 

 

 

 

 

 

 

 

 

11．已知f(x)＝x³＋x(x∈R)，

(1)判断f(x)在(－∞，＋∞)上的单调性，并证明；

(2)求证：满足f(x)＝a(a为常数)的实数x至多只有一个．

 

 

 

 

 

 

 

答案与解析

1．3　函数的基本性质

1．3.1　单调性与最大(小)值

课前预习

1．D　由已知，2k＋1＜0，解得k＜－.

2．C　如图所示，该函数的对称轴为x＝3，根据图象可知函数在(2,4)上是先递减再递增的．

3．C　由函数单调性的定义可知，若函数y＝f(x)在给定的区间上是增函数，则x₁－x₂与f(x₁)－f(x₂)同号，由此可知，选项A、B、D正确；

对于C，若x₁<x₂时，可有x₁＝a或x₂＝b，即f(x₁)＝f(a)或f(x₂)＝f(b)，故C不成立．

4．(1)37 ℃　(2)9　(3)3时～15时　(4)23 ℃～26 ℃

课堂巩固

1．C　∵a＋b>0，∴a>－b，b>－a.由函数的单调性可知，f(a)>f(－b)，f(b)>f(－a)．两式相加得C正确．

2．A　由二次函数的性质，可知4≤－(a－1)，解得a≤－3.

3．A　∵y＝x＋在定义域[，＋∞)上是增函数，∴y≥f()＝，即函数最小值为，无最大值，选A.

4．A　该函数的定义域为(－∞，－3]∪[1，＋∞)，函数f(x)＝x²＋2x－3的对称轴为x＝－1，由复合函数的单调性可知该函数在区间(－∞，－3]上是减函数．

5．减　由条件知a<0，b<0，∴－<0.此时，该二次函数是开口向下，对称轴小于零的二次函数．

6．－2x＋1　由一次函数f(x)是减函数，可设f(x)＝kx＋b(k<0)．

则f[f(x)]＝kf(x)＋b＝k(kx＋b)＋b＝k²x＋kb＋b，

∵f[f(x)]＝4x－1，

∴

解得

∴f(x)＝－2x＋1.

7．证明：(1)设0＜x₁＜x₂＜1，则x₂－x₁＞0，

f(x₂)－f(x₁)＝(x₂＋)－(x₁＋)

＝(x₂－x₁)＋(－)＝(x₂－x₁)＋

＝(x₂－x₁)(1－)＝，

若0＜x₁＜x₂＜1，则x₁x₂－1＜0，

故f(x₂)－f(x₁)＜0，∴f(x₂)＜f(x₁)．

∴f(x)＝x＋在(0,1)上是减函数．

8．解：设x₁，x₂是区间[－1,2]上的任意两个实数，且x₁<x₂，则

f(x₁)－f(x₂)＝3x₁＋2－3x₂－2＝3(x₁－x₂)．

由x₁<x₂，得x₁－x₂<0，

于是f(x₁)－f(x₂)<0，即f(x₁)<f(x₂)．

所以，函数f(x)＝3x＋2是区间[－1,2]上的增函数．

因此，函数f(x)＝3x＋2在区间[－1,2]的两个端点上分别取得最小值与最大值，即在x＝－1时取得最小值，最小值是－1，在x＝2时取得最大值，最大值是8.

课后检测

1．D　∵a²＋1－a＝(a－)²＋>0，

∴a²＋1>a.

又∵函数f(x)在(－∞，＋∞)上是减函数，

∴f(a²＋1)<f(a)．

2．A　由f(t)＝－t，当t∈(0，]时，f(t)是两个减函数的和，仍是减函数，故当t＝时，f(t)_min＝f()＝4－＝.

3.A　当m＝0时，y＝x＋5在[－2，＋∞)上是增函数，符合题意；当m<0时，－>0，显然不合题意；当m>0时，由－≤－2，得m≤，即0<m≤.

综上可知0≤m≤.

4．B　f(x)＝(x－2)²＋1，最小值1为x＝2时取得，最大值5为x＝0,4时取得，∴m的取值为[2,4]．

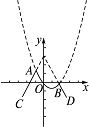
5．C　画图得到F(x)的图象：为射线AC、抛物线及射线BD三段，联立方程组得x_A＝2－，代入得F(x)的最大值为7－2，由图可得F(x)无最小值，从而选C.

6．D　由题意可知解得0<a≤2.

7.　设正方形周长为x，则圆的周长为1－x，半径r＝.

∴S_正＝()²＝，S_圆＝π·.

∴S_正＋S_圆＝(0<x<1)．

∴当x＝时有最小值．

8．(0，)　由题意，可得1＞1－a＞3a－1＞－1，即解得0＜a＜.

所以a的取值范围是(0，)．

9．解：因为自变量最高次数项的系数含有变量，所以应分类讨论．

(1)当k＝0时，f(x)＝－4x－8，它是[5,20]上的单调减函数．

(2)当k≠0时，有下列两种情形：

①k>0时，

当≥20，即0<k≤，f(x)在[5,20]上是减函数；

当≤5，即k≥时，f(x)在[5,20]上是增函数．

②k<0时，

当≥20时，不等式无解；

当≤5，即k<0时，f(x)在[5,20]上是减函数．

综上可知，实数k的取值范围是(－∞，]∪[，＋∞)．

10．解：f(x)＝＝＝1－.

设x₁，x₂是区间[1,3]上的任意两个实数，且x₁<x₂，则

f(x₁)－f(x₂)＝1－－1＋

＝－＝

＝.

由1≤x₁<x₂≤3，得x₁－x₂<0，(x₁＋1)(x₂＋1)>0，

于是f(x₁)－f(x₂)<0，即f(x₁)<f(x₂)．

所以，函数f(x)＝是区间[1,3]上的增函数．

因此，函数f(x)＝在区间[1,3]的两个端点上分别取得最大值与最小值，即在x＝1时取得最小值，最小值是0，在x＝3时取得最大值，最大值是.

点评：若函数在给定的区间上是单调函数，可利用函数的单调性求最值．若给定的单调区间是闭区间，则函数的最值在区间的两个端点处取得．

11．(1)解：f(x)在(－∞，＋∞)上是增函数．证明如下：

设x₁＜x₂，即x₁－x₂＜0.

∴f(x₁)－f(x₂)＝(x＋x₁)－(x＋x₂)

＝(x－x)＋(x₁－x₂)

＝(x₁－x₂)(x＋x₁x₂＋x＋1)

＝(x₁－x₂)[(x₁＋)²＋x＋1]＜0.

∴f(x₁)－f(x₂)＜0，即f(x₁)＜f(x₂)．

因此f(x)＝x³＋x在R上是增函数．

(2)证明：假设x₁＜x₂且f(x₁)＝f(x₂)＝a，由f(x)在R上递增，

∴f(x₁)＜f(x₂)，与f(x₁)＝f(x₂)矛盾．

∴原命题正确．

点评：利用定义判断函数单调性时，通常将作差后的因式变形成因式连乘积的形式、平方和的形式等．在因式连乘积的形式中，一定含有因式“x₁－x₂”，这也是指导我们化简的目标．差的符号是由自变量的取值范围、假定的大小关系及符号的运算法则共同决定的．